��Ŀ����
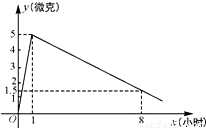
ijҽҩ�о���������һ����ҩ��������ҩЧʱ���֣�������˰��涨�������ã���ô��ҩ��2СʱʱѪҺ�к�ҩ����ߣ���ÿ����6�ˣ�1��=10-3���ˣ���������˥����10СʱʱѪҺ�к�ҩ��Ϊÿ����3�ˣ�ÿ����ѪҺ�к�ҩ��y���ˣ�����ʱ��x��Сʱ���ı仯��ͼ��ʾ��
�����˰��涨������ҩ��
��1���ֱ����x��2��x��2ʱ��y��x֮��ĺ�����ϵʽ��
��2�����ÿ����ѪҺ�к�ҩ��Ϊ4�˻�4������ʱ�����Ƽ���ʱ����Ч�ģ���ô�����Чʱ���Ƕ��
�����˰��涨������ҩ��
��1���ֱ����x��2��x��2ʱ��y��x֮��ĺ�����ϵʽ��
��2�����ÿ����ѪҺ�к�ҩ��Ϊ4�˻�4������ʱ�����Ƽ���ʱ����Ч�ģ���ô�����Чʱ���Ƕ��

�⣺��1����x��2ʱ����y=kx��
�ѣ�2��6��������ʽ����k=3��
��x��2ʱ��y=3x��
��x��2ʱ����y=kx+b��
�ѣ�2��6������10��3��������ʽ����k=- ��b=
��b= ��
��
��x��2ʱ��y=- x+
x+ ��
��
��2����y=4����y=3x����x1= ��
��
��y=4����y=- x+
x+ ����x2=
����x2= ��
��
��x2-x1=6Сʱ��
�������Чʱ��Ϊ6Сʱ��
�ѣ�2��6��������ʽ����k=3��
��x��2ʱ��y=3x��
��x��2ʱ����y=kx+b��
�ѣ�2��6������10��3��������ʽ����k=-
 ��b=
��b= ��
����x��2ʱ��y=-
 x+
x+ ��
����2����y=4����y=3x����x1=
 ��
����y=4����y=-
 x+
x+ ����x2=
����x2= ��
����x2-x1=6Сʱ��
�������Чʱ��Ϊ6Сʱ��

��ϰ��ϵ�д�
�����Ŀ
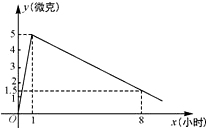 ��1.5�ˣ�ÿ����ѪҺ�к�ҩ��y���ˣ���ʱ��x��Сʱ���ı仯��ͼ��ʾ���ڳ��˰��涨������ҩ��
��1.5�ˣ�ÿ����ѪҺ�к�ҩ��y���ˣ���ʱ��x��Сʱ���ı仯��ͼ��ʾ���ڳ��˰��涨������ҩ��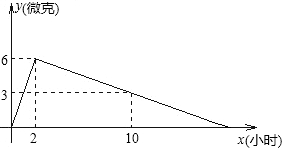 �ˣ�ÿ����ѪҺ�к�ҩ��y���ˣ�����ʱ��x��Сʱ���ı仯��ͼ��ʾ��
�ˣ�ÿ����ѪҺ�к�ҩ��y���ˣ�����ʱ��x��Сʱ���ı仯��ͼ��ʾ��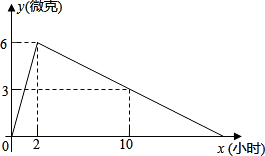 Һ�к�ҩ��Ϊÿ����3�ˣ�ÿ����ѪҺ�к�ҩ��y���ˣ����ҩ��ʱ��x��Сʱ���ı仯��ͼ��ʾ�������˰��涨������ҩ��
Һ�к�ҩ��Ϊÿ����3�ˣ�ÿ����ѪҺ�к�ҩ��y���ˣ����ҩ��ʱ��x��Сʱ���ı仯��ͼ��ʾ�������˰��涨������ҩ��