题目内容
 如图.点P是边长为1的正方形ABCD对角线AC上的一个动点(P不与A,C重合)且PE=PB
如图.点P是边长为1的正方形ABCD对角线AC上的一个动点(P不与A,C重合)且PE=PB (1)求证:PE⊥PD.
(2)设AP=x,四边形PECD的面积为y,求出y与x的关系式,并写出自变量的取值范围.
分析:(1)首先证明:△PBC≌△PDC,利用全等三角形的性质可得:∠GDP=∠EPF,而∠GDP+∠GPD=90°,那么可得出∠GPD+∠EPF=90°,由此可得出PD⊥PE.
(2)作出三角形的高,用未知数表示出即可.
(2)作出三角形的高,用未知数表示出即可.
解答:(1)证明∵四边形ABCD是正方形,AC为对角线,
∴BC=DC,∠BCP=∠DCP=45°.
∵PC=PC,
∴△PBC≌△PDC (SAS).
∴PB=PD,∠PBC=∠PDC.
∵PB=PE,
∴∠PBE=∠PEB,
∴∠PEB=∠PDC,
∴∠PEB+∠PEC=∠PDC+∠PEC=180°,
∴∠DPE=360°-(∠BCD+∠PDC+∠PEC)=90°,
∴PE⊥PD;
(2)过点P作PF⊥BC,垂足为F,则BF=FE.(如图3)
∵AP=x,AC=
,∠ACB=45°,PF⊥BC,
∴PC=
-x,PF=FC=1-
x,BF=FE=1-FC=1-(1-
x)=
x,
∴S△PBE=
EB•FP=BF•PF=-
x2+
x,
∴四边形PECD的面积为y=2S△BPC-S△PBE=2S△PBE=-x2+
x.
∴BC=DC,∠BCP=∠DCP=45°.
∵PC=PC,
∴△PBC≌△PDC (SAS).
∴PB=PD,∠PBC=∠PDC.
∵PB=PE,
∴∠PBE=∠PEB,
∴∠PEB=∠PDC,
∴∠PEB+∠PEC=∠PDC+∠PEC=180°,

∴∠DPE=360°-(∠BCD+∠PDC+∠PEC)=90°,
∴PE⊥PD;
(2)过点P作PF⊥BC,垂足为F,则BF=FE.(如图3)
∵AP=x,AC=
| 2 |
∴PC=
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
∴S△PBE=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴四边形PECD的面积为y=2S△BPC-S△PBE=2S△PBE=-x2+
| 2 |
点评:本题主要考查了正方形,矩形的性质,全等三角形的判定,列二次函数关系式,通过构建全等三角形来得出相关的边和角相等是解题的关键.

练习册系列答案
相关题目
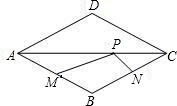 如图,点P是边长为1的菱形ABCD对角线AC上一个动点,点M,N分别为AB,BC边上的中点,则MP+NP的最小值是( )
如图,点P是边长为1的菱形ABCD对角线AC上一个动点,点M,N分别为AB,BC边上的中点,则MP+NP的最小值是( )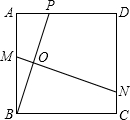 垂直平分线,与AB、BP、CD分别交于点M、O、N,设AP=x.
垂直平分线,与AB、BP、CD分别交于点M、O、N,设AP=x. 如图,点P是边长为1的菱形ABCD的对角线AC上一动点,点M、N分别是AB、BC中点,求MP+NP的最小值.
如图,点P是边长为1的菱形ABCD的对角线AC上一动点,点M、N分别是AB、BC中点,求MP+NP的最小值.