题目内容
解方程:
(1) ;
;
(2) .
.
解:(1)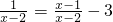
两边都乘以x-2,
得:1=x-1-3(x-2),
∴x=2,
经检验x=2是增根,
∴原方程无解;
(2) ,
,
两边都乘以x(x-1),
得:3(x-1)+6x=7,
∴9x=10,
∴ ,
,
经检验 是原方程的根,
是原方程的根,
∴原方程的根是 .
.
分析:本题考查解分式方程的能力,因为(2-x)=-(x-2),所以可得:
(1)中方程最简公分母为(x-2);
(2)中因为x2-x=x(x-1),所以可得方程最简公分母为:x(x-1),然后方程两边同乘最简公分母将分式方程转化为整式方程求解,不要忽略检验.
点评:(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.
(2)解分式方程一定注意要验根.
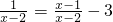
两边都乘以x-2,
得:1=x-1-3(x-2),
∴x=2,
经检验x=2是增根,
∴原方程无解;
(2)
 ,
,两边都乘以x(x-1),
得:3(x-1)+6x=7,
∴9x=10,
∴
 ,
,经检验
 是原方程的根,
是原方程的根,∴原方程的根是
 .
.分析:本题考查解分式方程的能力,因为(2-x)=-(x-2),所以可得:
(1)中方程最简公分母为(x-2);
(2)中因为x2-x=x(x-1),所以可得方程最简公分母为:x(x-1),然后方程两边同乘最简公分母将分式方程转化为整式方程求解,不要忽略检验.
点评:(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.
(2)解分式方程一定注意要验根.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目