Question

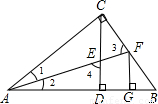
如图，CD为Rt△ABC斜边上的高，∠BAC的平分线分别交CD、CB于点E、F，FG⊥AB，垂足为G，则CF__________FG，∠1+∠3=__________度，∠2+∠4=__________度，∠3__________∠4，CE__________CF.

 

Answer 1

【答案】

=，90，90，=，=

【解析】

试题分析：根据角平分线的性质，三角形的内角和定理，同角或等角的余角相等填空即可.

∵CD为Rt△ABC斜边上的高，∠BAC的平分线分别交CD、CB于点E、F，FG⊥AB

∴CF=FG，∠1+∠3=90度，∠2+∠4=90度，

∴∠3=∠4

∵∠4=∠CEF

∴∠3=∠CEF

∴CE=CF.

考点：角平分线的性质，三角形的内角和定理，同角或等角的余角相等，等角对等边

点评：此类题目综合性强，知识点多，在中考中比较常见，常以填空题、选择题形式出现，难度不大，需多加关注.