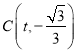题目内容
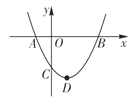
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 为坐标原点.抛物线
为坐标原点.抛物线![]() 分别交
分别交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,
,![]() .
.
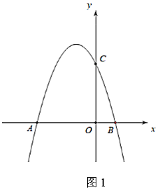
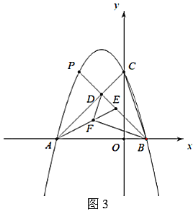
(1)求该抛物线的解析式.
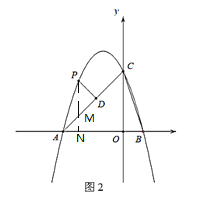
(2)如图2,点![]() 为第二象限抛物线上一点,过点
为第二象限抛物线上一点,过点![]() 作
作![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长度为
的长度为![]() ,求
,求![]() 与
与![]() 的函数关系式(不要求写出自变量
的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
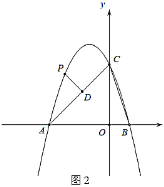
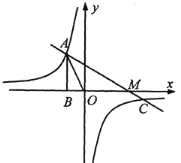
(3)在(2)的条件下,当直线![]() 经过点
经过点![]() 时,如图3,点
时,如图3,点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的长.
的长.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)利用OA=OC,待定系数法求解二次函数解析式.
(2)过P作![]() 轴的垂线,用锐角三角函数建立PD与PM之间的联系,用二次函数与一次函数求解PM的长度,从而得到答案.
轴的垂线,用锐角三角函数建立PD与PM之间的联系,用二次函数与一次函数求解PM的长度,从而得到答案.
(3)延长DF交AB于N,过F,D作好AB的垂线,利用面积与相似三角形求解FN,,DN的数量关系,再利用![]() ,找到
,找到![]() ,利用相似三角形性质表示AN的长,最后化归到直角三角形DNQ中,利用勾股定理得到答案.
,利用相似三角形性质表示AN的长,最后化归到直角三角形DNQ中,利用勾股定理得到答案.
解:(1)因为:![]() ,
,
所以点C![]() ,所以
,所以![]() ,
,
又因为![]()
所以![]() ,把
,把![]() 代入解析式得:
代入解析式得:
![]() ,即
,即![]()
解得:![]() (舍去),所以
(舍去),所以![]() ,
,
所以抛物线为![]()
(2)如图,过P作![]() 轴与N,交AC于M,又
轴与N,交AC于M,又![]() ,
,![]()
所以![]() .
.
因为![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]()
所以![]()
由(1)得![]() ,所以 直线AC为
,所以 直线AC为![]() ,
,
因为![]() ,
,![]() 轴,
轴,
所以![]()
所以![]()
所以![]()
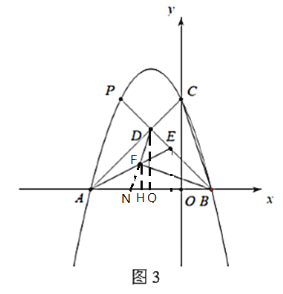
(3)如图,延长DF交AB于N,过F,D分别作![]() ,垂足分别为H,Q,因为抛物线为
,垂足分别为H,Q,因为抛物线为![]() ,所以B(1,0),A(-3,0)
,所以B(1,0),A(-3,0)
所以AB=4,因为![]() 的面积为
的面积为![]() ,
,
所以![]() ,所以
,所以![]() ,
,
因为A(-3,0),C(0,-3),![]()
所以![]()
因为![]()
所以![]()
所以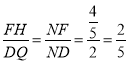
设![]() ,则
,则![]()
因为![]() ,
,![]() ,
,
所以![]()
所以![]() ,
,
又因为![]()
所以![]()
所以![]() 所以
所以![]() ,
,
所以![]()
在直角三角形DNQ中,![]()
所以![]()
解得:![]() ,(负根舍去)
,(负根舍去)
所以![]()

【题目】某水果店计划进A,B两种水果共140千克,这两种水果的进价和售价如表所示
进价 | 售价 | |
A种水果 | 5 | 8 |
B种水果 | 9 | 13 |
![]() 若该水果店购进这两种水果共花费1020元,求该水果店分别购进A,B两种水果各多少千克?
若该水果店购进这两种水果共花费1020元,求该水果店分别购进A,B两种水果各多少千克?
![]() 在
在![]() 的基础上,为了迎接春节的来临,水果店老板决定把A种水果全部八折出售,B种水果全部降价
的基础上,为了迎接春节的来临,水果店老板决定把A种水果全部八折出售,B种水果全部降价![]() 出售,那么售完后共获利多少元?
出售,那么售完后共获利多少元?