题目内容
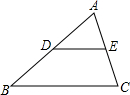
在△ABC中,AB=AC=a,BC=b,∠A=36°,记m=
,n=
,p=
,则m、n、p的大小关系为( )
| a+b |
| a-b |
| (a+b)2 |
| ab |
| a3 |
| b3 |
| A.m>n>p | B.p>m>n | C.n>p>m | D.m=n=p |
作底角B的角平分线交AC于D,
易推得△BCD∽△ABC,
所以
=
,即CD=
,AD=a-
=b(△ABD是等腰三角形)
因此得a2-b2=ab,
∴n=
=
=
=m,
p=
=
=
=m,
∴m=n=p.
故选D.

易推得△BCD∽△ABC,
所以
| a |
| b |
| b |
| CD |
| b2 |
| a |
| b2 |
| a |
因此得a2-b2=ab,
∴n=
| (a+b)2 |
| ab |
| (a+b)2 |
| a2-b2 |
| a+b |
| a-b |
p=
| a3 |
| b3 |
| (b2+ab)•a |
| (a2-ab)•b |
| a+b |
| a-b |
∴m=n=p.
故选D.


练习册系列答案
相关题目