题目内容
(1)| 12 |
| 3 |
|
| 1 |
| 2 |
(2)解方程:x2-3x-4=0.
分析:(1)利用先算乘方再算乘除最后算加减的运算法则进行有理数的混合运算即可.
(2)将方程的左边分解为(x-4)(x+1)即可求得方程的解.
(2)将方程的左边分解为(x-4)(x+1)即可求得方程的解.
解答:解:(1)
-(
+1)2+
+(-3)2÷(
)-1
=2
-4-2
+
+9÷2
=2
-4-2
+
+4.5
=
+0.5;
(2)∵x2-3x-4=0,
∴(x-4)(x+1)=0,
∴x-4=0或x+1=0,
解得x1=4,x2=-1.
| 12 |
| 3 |
|
| 1 |
| 2 |
=2
| 3 |
| 3 |
| ||
| 2 |
=2
| 3 |
| 3 |
| ||
| 2 |
=
| ||
| 2 |
(2)∵x2-3x-4=0,
∴(x-4)(x+1)=0,
∴x-4=0或x+1=0,
解得x1=4,x2=-1.
点评:本题是基础题,考查了一元二次方程的解法.解题的关键是正确的利用十字相乘法进行因式分解.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
直角三角形两直角边长度为5,12,则斜边上的高( )
| A、6 | ||
| B、8 | ||
C、
| ||
D、
|
关于x的一元二次方程(a-1)x2+a2-1=0的一个根是x=0,则a等于( )
| A、1 | ||
| B、-1 | ||
| C、±1 | ||
D、
|
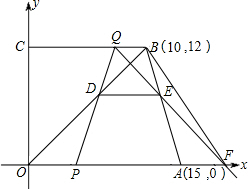 动时间为t(单位:秒).
动时间为t(单位:秒).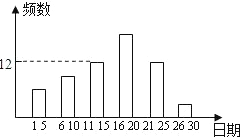 出一张卡片,抽到第四组作品的概率是多少?
出一张卡片,抽到第四组作品的概率是多少?