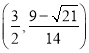题目内容
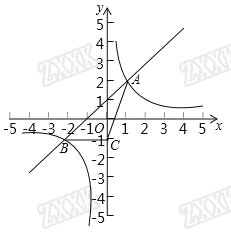
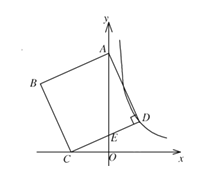
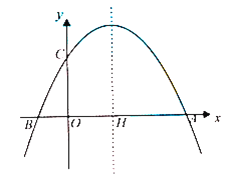
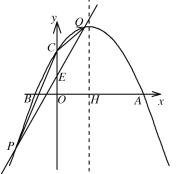
【题目】如图，在平面直角坐标系中，抛物线
的图象与x轴交于
，B两点，与y轴交于点
，对称轴
与x轴交于点H.
（1）求抛物线的函数表达式
（2）直线
与y轴交于点E，与抛物线交于点P,Q（点P在y轴左侧，点Q 在y轴右侧），连接CP，CQ，若
的面积为
，求点P，Q的坐标.
（3）在（2）的条件下，连接AC交PQ于G，在对称轴上是否存在一点K，连接GK，将线段GK绕点G逆时针旋转90°，使点K恰好落在抛物线上，若存在，请直接写出点K的坐标不存在，请说明理由.
【答案】（1）
；（2）
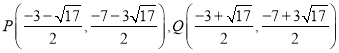；（3）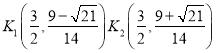
【解析】
（1）利用对称轴和A点坐标可得出
，再设
，代入C点坐标，求出a的值，即可得到抛物线解析式；
（2）求C点和E点坐标可得出CE的长，再联立直线与抛物线解析式，得到
，设点P,Q的横坐标分别为
，利用根与系数的关系求出
，再根据
的面积
可求出k的值，将k的值代入方程求出，即可得到P、Q的坐标；
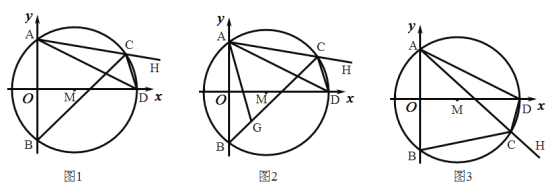
（3）先求直线AC解析式，再联立直线PQ与直线AC，求出交点G的坐标，设
，
,过G作MN∥y轴，过K作KN⊥MN于N，过K'作K'M⊥MN于M，然后证明△MGK'≌△NKG，推出MK'=NG，MG=NK，建立方程求出
的坐标，再代入抛物线解析式求出m的值，即可得到K的坐标.
解：（1）∵抛物线对称轴
，点
∴
设抛物线的解析式为
将点
代入解析式得：
，
解得
，
∴抛物线的解析式为
,即
（2）当x=0时，
∴C点坐标为(0,2)，OC=2
直线
与y轴交于点E，
当x=0时，
∴点
，OE=1
∴
联立和得：
整理得：
设点P,Q的横坐标分别为
则是方程的两个根,
∴
∴
∴的面积
解得
（舍）
将k=3代入方程得：
解得：
∴
∴
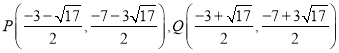
（3）存在，
设AC直线解析式为
，
代入A(4,0)，C(0,2)得
，解得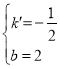
，
∴AC直线解析式为
联立直线PQ与直线AC得
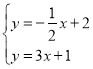，解得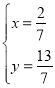
∴
设，,
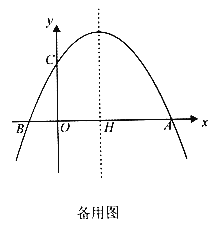
如图，过G作MN∥y轴，过K作KN⊥MN于N，过K'作K'M⊥MN于M，
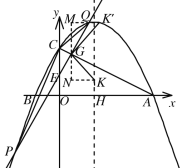
∵∠KGK'=90°，
∴∠MGK'+∠NGK=90°
又∵∠NKG+∠NGK=90°
∴∠MGK'=∠NKG
在△MGK'和△NKG中，
∵∠M=∠N=90°，∠MGK'=∠NKG，GK'=GK
∴△MGK'≌△NKG（AAS）
∴MK'=NG，MG=NK
∴
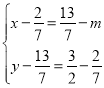，解得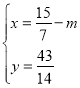
即K'坐标为(
,
)
代入得：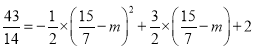
解得：
∴K的坐标为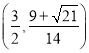
或
