题目内容
直线y=mx+1与抛物线y=2x2-8x+k+8相交于点（3，4），则m、k值为
- A.
- B.
- C.
- D.
C
分析：将点（3，4）分别代入直线y=mx+1与抛物线y=2x2-8x+k+8即可得到m、k的值．
解答：将点（3，4）分别代入直线y=mx+1与抛物线y=2x2-8x+k+8得，
3m+1=4，解得m=1；
2×9-8×3+k+8=4，解得k=2；
可得，
故选C．
点评：本题考查了二次函数图象上点的坐标特征和一次函数图象上点的坐标特征，要知道，函数图象上的点符合函数解析式．
分析：将点（3，4）分别代入直线y=mx+1与抛物线y=2x2-8x+k+8即可得到m、k的值．
解答：将点（3，4）分别代入直线y=mx+1与抛物线y=2x2-8x+k+8得，
3m+1=4，解得m=1；
2×9-8×3+k+8=4，解得k=2；
可得
，故选C．
点评：本题考查了二次函数图象上点的坐标特征和一次函数图象上点的坐标特征，要知道，函数图象上的点符合函数解析式．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
（2012•遂宁）已知：如图，直线y=mx+n与抛物线
于A、B两点（点A在点B左侧），与y轴交于点C．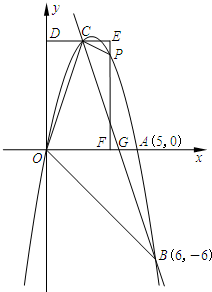
如图，抛物线y=ax2+bx+c经过点A（5，0）、B（6，-6）和原点O，过点B的直线y=mx+n与抛物线相交于点C（2，y）．过点C作平行于x轴的直线交y轴于点D，在抛物线对称轴右侧位于直线DC下方的抛物线上，任取一点P，过点P作直线PF平行于y轴，交直线DC于点E，交x轴于点F．
（2013•贵阳）已知：直线y=ax+b过抛物线y=-x2-2x+3的顶点P，如图所示．