题目内容
在用计算器计算一个多边形的内角和时,小明的结果为2115°,小芳立即判断他的结果是错误的,小明仔细地复算了一遍,果然发现自己把一个角的度数输入了两遍.根据以上事实,请你判定该多边形为分析:n边形的内角和是(n-2)•180°,因而内角和一定是180度的倍数.而多边形的内角一定大于0,并且小于180度,因而内角和再加上一个内角的值,这个值除以180度,所得数值比边数要大,大的值小于1.
解答:解:设(x-2)•180=2115,解得x=13.75.
当x=13时,(13-2)×180°=1980°,多加了一个135°的内角.
因而多边形的边数是13,该多边形为十三边形.
当x=13时,(13-2)×180°=1980°,多加了一个135°的内角.
因而多边形的边数是13,该多边形为十三边形.
点评:正确理解多边形的内角和是180度的整数倍,以及多边形的角的范围,是解题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目

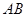 绕它的中点
绕它的中点 ,按逆时针方向旋转30°,则线段
,按逆时针方向旋转30°,则线段 (精确到0.01).
(精确到0.01). 绕它的中点
绕它的中点 ,按逆时针方向旋转30°,则线段
,按逆时针方向旋转30°,则线段 (精确到0.01).
(精确到0.01).