题目内容
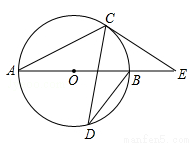
如图，AB是⊙O的直径，C．D是⊙O上一点，∠CDB=20°，过点C作⊙O的切线交AB的延长线于点E，则∠E等于（ ）
（A）40° （B）50° （C）60° （D）70°
B
【解析】
试题分析：如图所示，连接OC。
由∠BOC与∠CDB是弧
所对的圆心角与圆周角，可求∠BOC=2∠CDB.由∠CDB=20°，得∠BOC=40°，又由CE为圆O的切线，∠OCE=90°.则∠E=90°﹣40°=50°.
故选B.
考点：圆的切线，圆周角，圆心角
练习册系列答案
名校课堂系列答案
相关题目
，
）、B（
，1）、C（0，
）．
，画出旋转后得到的△A1B1C；
，
）与
（-8，
）关于原点对称，则Ａ点的坐标为 
的值为 ，表示“月平均收入在2000元以内”的部分所对应扇形的圆心角的度数是 ；