题目内容
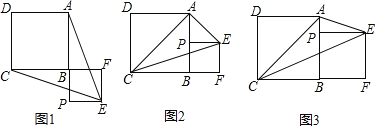
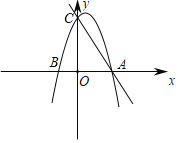
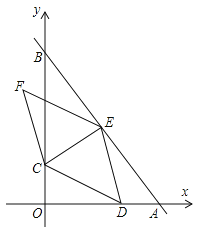
【题目】如图，在平面直角坐标系中，直线AB与x轴，y轴分别交于点A（6，0），B（0，8），点C在OB上运动，过点C作CE⊥AB于点E；D是x轴上一点，作菱形CDEF，当顶点F恰好落在y轴正半轴上时，点C的纵坐标的值为______．
【答案】
【解析】
设C（0，m）．由DF∥AB，CF＝BF＝DE＝
，根据cos∠CBE＝
，可得BE＝
，推出AE＝10，由DE∥OB，推出∠ADE＝∠AOB＝90°，推出sin∠DAE＝
，可得
，解方程即可解决问题．
解：如图，设C（0，m）．
∵四边形EFCD是菱形，
∴DF⊥CE，CP＝PE，
∵CE⊥AB，
∴DF∥AB，CF＝BF＝DE＝
∵cos∠CBE＝，
∴BE＝，
∴AE＝10，
∵DE∥OB，
∴∠ADE＝∠AOB＝90°，
∴sin∠DAE＝，
∴，
∴m＝ ，
故答案为：．
练习册系列答案
文敬图书课时先锋系列答案
相关题目
