Question

【题目】（1）如图，点、 分别在正方形 的边、上，，，，连结，把 绕点逆时针旋转至，使与重合.求的面积.

（2）如图，四边形中，，，点、分别在、边上，且，求证：.

Answer 1

【答案】（1）15；（2）见解析

【解析】

（1）首先由旋转的性质，得出∠BAE=∠DAG，然后通过等角转换得出∠GAF=∠EAF =45°，根据SAS判定△AEF≌△AGF，两个三角形面积相等，即可得解；

（2）首先延长CB至G，使得BG=FD，连接AG，然后由得出∠GBA=∠FDA，再由BG=DF，可判定△ABG≌△ADF，进而得出∠BAG=∠DAF，AG=AF，又由得出∠EAG=∠EAF，加上AE=AE，可判定△AGE≌△AFE，得出GE=EF，即可得证.

（1）由已知得，∠BAE=∠DAG

∵∠BAE+∠EAD=90°

∴∠DAG+∠EAD=90°

又∵∠EAF=45°

∴∠GAF=∠EAF =45°

又∵AE=AG，AF=AF

∴△AEF≌△AGF（SAS）

∴EF=GF=5

∴

（2）延长CB至G，使得BG=FD，连接AG，如图所示

∵

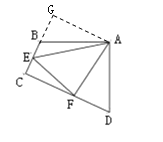
∴∠GBA=∠FDA

又∵BG=DF，

∴△ABG≌△ADF（SAS）

∴∠BAG=∠DAF，AG=AF

又∵

∴∠DAF+∠EAB=∠EAF

∴∠BAG+∠EAB=∠EAF

∴∠EAG=∠EAF

又∵AE=AE

∴△AGE≌△AFE（SAS）

∴GE=EF

∴BE+BG=EF

∴