题目内容
(1)解方程组:
(2)求不等式组 的整数解.
的整数解.
解:(1)原方程组化简为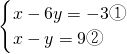 ,
,
②-①,得5y=12,y= ,
,
将y= 代入②,得x=
代入②,得x= ,
,
所以原方程组的解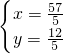 ;
;
(2)由2(x-1)+3≤3x,得x≥1,
由 +4>x,得x<
+4>x,得x< ,
,
所以1≤x< ,
,
所以不等式组 的整数解为1,2,3.
的整数解为1,2,3.
分析:(1)先将方程组化简为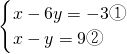 ,再②-①,消去未知数x,得到y的一元一次方程,求出y的值,进而求出x即可;
,再②-①,消去未知数x,得到y的一元一次方程,求出y的值,进而求出x即可;
(2)首先利用不等式的基本性质解不等式组,再从不等式组的解集中找出适合条件的整数即可.
点评:本题考查了(1)二元一次方程组的解法,解二元一次方程组的基本思想是消元,即化“二元”为“一元”;
(2)一元一次不等式组的整数解,正确解不等式,求出解集是解答本题的关键.解不等式应根据不等式的基本性质.
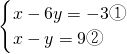 ,
,②-①,得5y=12,y=
 ,
,将y=
 代入②,得x=
代入②,得x= ,
,所以原方程组的解
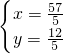 ;
;(2)由2(x-1)+3≤3x,得x≥1,
由
 +4>x,得x<
+4>x,得x< ,
,所以1≤x<
 ,
,所以不等式组
 的整数解为1,2,3.
的整数解为1,2,3.分析:(1)先将方程组化简为
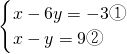 ,再②-①,消去未知数x,得到y的一元一次方程,求出y的值,进而求出x即可;
,再②-①,消去未知数x,得到y的一元一次方程,求出y的值,进而求出x即可;(2)首先利用不等式的基本性质解不等式组,再从不等式组的解集中找出适合条件的整数即可.
点评:本题考查了(1)二元一次方程组的解法,解二元一次方程组的基本思想是消元,即化“二元”为“一元”;
(2)一元一次不等式组的整数解,正确解不等式,求出解集是解答本题的关键.解不等式应根据不等式的基本性质.

练习册系列答案
相关题目
 (1)解方程组:
(1)解方程组: