题目内容

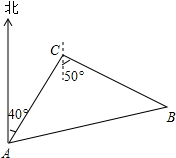如图，某巡逻艇在A处发现北偏东40°相距9海里的C处有一艘走私船，正沿南偏东50°的方向以10海里/时的速度向我海岸行驶，巡逻艇立即以14海里/时的速度沿着直线方向追去，问需要多少时间才能追赶上该走私船？巡逻艇应该沿什么方向去追？

解：由题意得，∠ACB=90°，
设经过t小时在点C处刚好追上走私船，
依题意得：AB=14t，BC=10t，
在Rt△ABC中，9²+（10t）²=（14t）²，
解得：t=± $\text{[math]}$ （负值舍去），
∵tan∠BAC= $\text{[math]}$ = $\text{[math]}$ ，
∴∠BAC≈46°．
∴∠巡逻艇应该沿北偏东86°去追．
分析：先设经过t小时在点B处刚好追上走私船，进而可表示出AB和BC，进而根据勾股定理得到t的值，在Rt△ABC中利用正弦定理求得sin∠BAC的值，求出∠BAC，继而确定追赶方向．
点评：本题主要考查了解三角形的实际应用．解答关键是运用三角函数的基础知识解决实际的问题．

练习册系列答案

优佳学案云南省初中学业水平考试总复习系列答案

相关题目

如图所示，某海关缉私巡逻艇在海上执行巡逻任务时，发现在其所处位置O点的正北方向10海里的A点有一涉嫌走私船只，正以10

海里/时的速度向正东方向航行，为了迅速实施检查，巡逻艇调整好航向，以20海里/时的速度追赶，在涉嫌走私船只不改变航向和航速的前提下，问：
（1）需要几小时才能追上？（点B为追上时的位置）
（2）确定巡逻艇的追赶方向．

如图，南北方向PQ以东为我国的领海，以西为公海．某天晚上10时28分，我边防反偷渡巡逻艇101号在A处发现其正西方向的C处有一可疑船只正向我沿海靠近，便立即通知正在PQ上B处巡逻的103号艇注意其动向．经观测发现，A、C之间的距离为10海里，A、B之间的距离为6海里，B、C之间的距离为8海里．若该可疑船只的速度为12.8海里/时，则该可疑船只最早在何时进入我国领海？

如图所示，某海关缉私巡逻艇在海上执行巡逻任务时，发现在其所处位置O点的正北方向10海里的A点有一涉嫌走私船只，正以 $数学公式$ 海里/时的速度向正东方向航行，为了迅速实施检查，巡逻艇调整好航向，以20海里/时的速度追赶，在涉嫌走私船只不改变航向和航速的前提下，问：
（1）需要几小时才能追上？（点B为追上时的位置）
（2）确定巡逻艇的追赶方向．

试题分类