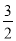��Ŀ����
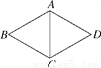
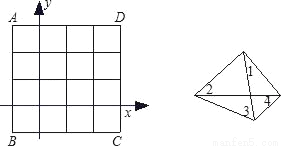
��ͼ������ƽ��ֱ������ϵ�е�������ABCD�ı߳�Ϊ4����������ʵ�飺����һö���ȵ������������ӣ���ͼ�������ĸ����㣬���������ֱ���1��2��3��4����ÿ�����㳯�ϵĻ�������ͬ�ģ������������Σ������ӳ��ϵĵ�����Ϊֱ������ϵ�е�P�����꣨��һ�εĵ���Ϊ�����꣬�ڶ��εĵ���Ϊ�����꣩��
��1�����P�������������ϣ����߽磬��ͬ���ĸ��ʣ�
��2����������ABCDƽ��������λ���Ƿ����һ��ƽ�ƣ�ʹ��P�������������ϵĸ���Ϊ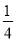 �������ڣ�ָ�����е�һ��ƽ�Ʒ�ʽ���������ڣ�˵�����ɣ�
�������ڣ�ָ�����е�һ��ƽ�Ʒ�ʽ���������ڣ�˵�����ɣ�
��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ


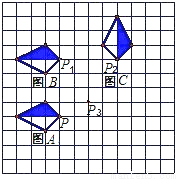
 ��
��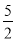 ����
����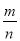 ����(�� ��)
����(�� ��)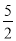 B.
B. 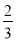 C.
C. 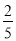 D.
D.