题目内容
如图，AB是⊙O直径，CD是⊙O的弦，∠ABD=50°；求∠BCD的大小．
解：∵AB是⊙O直径，
∴∠ADB=90°，
∵∠ABD=50°，
∴∠BAD=90°-∠ABD=40°，
∴∠BCD=∠BAD=40°．
分析：由AB是⊙O直径，根据直径所对的圆周角是直角，即可得∠ADB的度数，继而求得∠A的度数，又由圆周角定理，即可求得答案．
点评：此题考查了圆周角定理．此题难度不大，注意掌握数形结合思想的应用．
∴∠ADB=90°，
∵∠ABD=50°，
∴∠BAD=90°-∠ABD=40°，
∴∠BCD=∠BAD=40°．
分析：由AB是⊙O直径，根据直径所对的圆周角是直角，即可得∠ADB的度数，继而求得∠A的度数，又由圆周角定理，即可求得答案．
点评：此题考查了圆周角定理．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
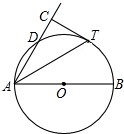如图，AB是⊙O直径，D为⊙O上一点，AT平分∠BAD交⊙O于点T，过T作AD的垂线交AD的延长线于点C．
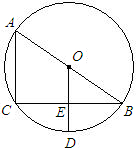如图，AB是⊙O直径，BC是弦，OD⊥BC于E交弧BC于D．根据中考改编
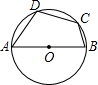如图，AB是⊙O直径，C、D是⊙O上的两点，若∠BAC=20°，
如图，AB是⊙O直径，OB=6，弦CD=10，则弦心距OP的长为（ ）
如图，AB是⊙O直径，弦CD交AB于E，∠AEC=45°，AB=2．设AE=x，CE2+DE2=y．下列图象中，能表示y与x的函数关系是的（ ）