Question

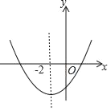
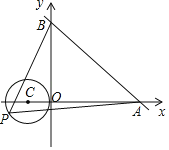
【题目】如图，直线y＝﹣x+6与x轴、y轴分别交于A、B两点，点P是以C（﹣1，0）为圆心，1为半径的圆上一点，连接PA，PB，则△PAB面积的最大值为_____．

Answer 1

【答案】10

【解析】

求出A、B的坐标，根据勾股定理求出AB，求出点C到AB的距离，即可求出圆C上点到AB的最大距离，根据面积公式求出即可．

作CH⊥AB于H交⊙O于E、F．

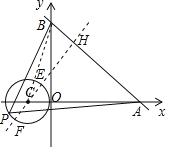
∵C（﹣1，0），直线AB的解析式为，

∴直线CH的解析式为，

由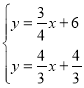解得，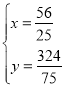

∴H，

∴CH═3，

∵A（4，0），B（0，3），

∴OA＝4，OB＝3，AB＝5，

∴S△ABC＝ABCH＝OBOC+OAOB，

∴×5CH＝×3×1+×3×4，

∴CH＝3，

∴FH＝3+1＝4，即⊙C上到AB的最大距离为4，

∴△PAB面积的最大值＝×5×4＝10，

故答案为：10．