题目内容
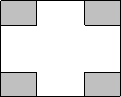 22、某小区有一长100m,宽80m的空地,现将其建成花园广场,设计图案如下,阴影区域为绿化区(四块绿化区是全等矩形),空白区域为活动区,且四周出口一样宽,宽度不小于50m,不大于60m.预计活动区每平方米造价60元,绿化区每平方米造价50元.设一块绿化区的长边为x m.
22、某小区有一长100m,宽80m的空地,现将其建成花园广场,设计图案如下,阴影区域为绿化区(四块绿化区是全等矩形),空白区域为活动区,且四周出口一样宽,宽度不小于50m,不大于60m.预计活动区每平方米造价60元,绿化区每平方米造价50元.设一块绿化区的长边为x m.(1)用x表示一块绿化区的短边;
(2)写出工程总造价y与x的函数关系式;
(3)要完成工程任务,最少需投资多少万元?
分析:(1)根据一块绿化区的长边为x m,根据空地长为100m可先求出口的宽,且四周出口一样宽,再根据空地的宽为80m,就可求出绿化区的短边.
(2)总造价=绿化区的造价+活动区的造价,且用x分表表示出绿化区和活动区的面积,根据预计活动区每平方米造价60元,绿化区每平方米造价50元可列出函数式.
(3)根据出口宽度不小于50m,不大于60m可求出自变量的取值范围,根据取值范围可求出最值.
(2)总造价=绿化区的造价+活动区的造价,且用x分表表示出绿化区和活动区的面积,根据预计活动区每平方米造价60元,绿化区每平方米造价50元可列出函数式.
(3)根据出口宽度不小于50m,不大于60m可求出自变量的取值范围,根据取值范围可求出最值.
解答:解:(1)设一块绿化区的长边为xm,
[80-(100-2x)]÷2=x-10.
故一块绿化区的短边为:x-10.
(2)一块绿化区的长边为xm,工程总造价y,
y=50×4x(x-10)+60[80×100-4x(x-10)]=-40x2+400x+480000,
(3)y=-40(x-5)2+481000,
∵50≤100-2x≤60,
∴20≤x≤25(1分)
∴当x=25时,y有最小值为465000元,即该小区至少投资46.5万元.
[80-(100-2x)]÷2=x-10.
故一块绿化区的短边为:x-10.
(2)一块绿化区的长边为xm,工程总造价y,
y=50×4x(x-10)+60[80×100-4x(x-10)]=-40x2+400x+480000,
(3)y=-40(x-5)2+481000,
∵50≤100-2x≤60,
∴20≤x≤25(1分)
∴当x=25时,y有最小值为465000元,即该小区至少投资46.5万元.
点评:本题考查二次函数的应用,本题中关键设出一块绿化区的长边能表示出短边,根据活动区每平方米造价60元,绿化区每平方米造价50元求出总造价y和x的函数式,根据题意求出自变量的取值范围,根据函数式的特点求出最值即x越大时函数值越小.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
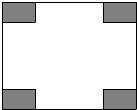 某小区有一长100m,宽80m的空地,现将其建成花园广场,设计图案如下,阴影区域为绿化区(四块绿化区是全等矩形),空白区域为活动区,且四周出口一样宽,宽度不小于50m,不大于60m.预计活动区每平方米造价60元,绿化区每平方米造价50元.设每块绿化区的长边为x m,短边为y m,工程总造价为w元.
某小区有一长100m,宽80m的空地,现将其建成花园广场,设计图案如下,阴影区域为绿化区(四块绿化区是全等矩形),空白区域为活动区,且四周出口一样宽,宽度不小于50m,不大于60m.预计活动区每平方米造价60元,绿化区每平方米造价50元.设每块绿化区的长边为x m,短边为y m,工程总造价为w元. 某小区有一长100m,宽80m的空地,现将其建成花园广场,设计图案如下:阴影区域为绿化区(四块绿化区是全等矩形),空白区域为活动区,且四周出口一样宽,宽度不小于50m,不大于60m.预计活动区每平方米造价60元,绿化区每平方米造价50元.
某小区有一长100m,宽80m的空地,现将其建成花园广场,设计图案如下:阴影区域为绿化区(四块绿化区是全等矩形),空白区域为活动区,且四周出口一样宽,宽度不小于50m,不大于60m.预计活动区每平方米造价60元,绿化区每平方米造价50元.
 )
)