题目内容
平行四边形周长为20厘米,若被两条对角线分成的相邻两个小三角形周长和为25厘米,则对角线之和为________厘米.
15
分析:根据平行四边形的性质可知,平行四边形的对边相等,可得一组邻边的和为10,所以对角线的长可求解.
解答: 解:设平行四边形的两条边是x,y,
解:设平行四边形的两条边是x,y,
∴2x+2y=20,即x+y=10,
∵两个小三角形周长和为25cm,
∴x+y+(2AO+BO+OD)=25,
把x+y=10代入得到2AO+BD=25-10=15cm.
即AC+BD=15cm.
故答案为15.
点评:本题主要考查了平行四边形的基本性质,并利用性质解题.平行四边形基本性质:①平行四边形两组对边分别平行;②平行四边形的两组对边分别相等;③平行四边形的两组对角分别相等;④平行四边形的对角线互相平分.
分析:根据平行四边形的性质可知,平行四边形的对边相等,可得一组邻边的和为10,所以对角线的长可求解.
解答:
 解:设平行四边形的两条边是x,y,
解:设平行四边形的两条边是x,y,∴2x+2y=20,即x+y=10,
∵两个小三角形周长和为25cm,
∴x+y+(2AO+BO+OD)=25,
把x+y=10代入得到2AO+BD=25-10=15cm.
即AC+BD=15cm.
故答案为15.
点评:本题主要考查了平行四边形的基本性质,并利用性质解题.平行四边形基本性质:①平行四边形两组对边分别平行;②平行四边形的两组对边分别相等;③平行四边形的两组对角分别相等;④平行四边形的对角线互相平分.

练习册系列答案
相关题目
 如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD交BC于点E,若平行四边形ABCD的周长为20,则△CDE的周长为
如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD交BC于点E,若平行四边形ABCD的周长为20,则△CDE的周长为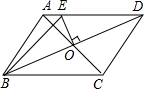 (2012•乌鲁木齐)如图,在周长为20的平行四边形ABCD中,AB<AD,AC与BD交于点O,OE⊥BD,交AD于点E,则△ABE的周长为
(2012•乌鲁木齐)如图,在周长为20的平行四边形ABCD中,AB<AD,AC与BD交于点O,OE⊥BD,交AD于点E,则△ABE的周长为