Question

【题目】已知点E是正方形ABCD内一点，连接AE，CE.

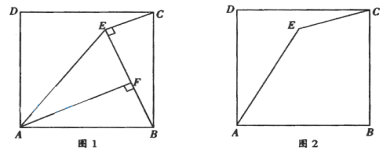
(1)如图1，连接，过点作于点，若，，四边形的面积为.

①证明:;

②求线段的长.

(2)如图2，若，，，求线段，的长.

Answer 1

【答案】（1）①证明见解析；②AE=；（2）,.

【解析】

（1）①由正方形性质可得：AB＝BC，∠ABC＝90°，再证明△ABF≌△BCE（AAS）即可；②设AF＝BE＝m，由四边形ABCE的面积＝△ABE面积＋△BCE面积，可列方程求出AF，然后利用勾股定理可得AE的长；

（2）过A作AF⊥CE于F，连接AC，由，可得，再由△AEF、△ABC均为等腰直角三角形及勾股定理即可求得AE和CE的长．

解：（1）①证明：∵ABCD是正方形，

∴AB＝BC，∠ABC＝90°

∴∠ABF＋∠CBE＝90°

∵AF⊥BE

∴∠AFB＝∠BEC＝90°

∴∠ABF＋∠BAF＝90°

∴∠BAF＝∠CBE

∴△ABF≌△BCE（AAS）

∴AF＝BE；

②∵△ABF≌△BCE（AAS）

∴BF＝CE＝2，设AF＝BE＝m，

∵四边形ABCE的面积为．

∴S△BCE＋S△ABE＝，即×2m＋m2＝，

解得：m1＝5，m2＝7（舍），

∴AF＝BE＝5，EF＝3

∴AE＝；

（2）如图2，过A作AF⊥CE于F，连接AC，则∠F＝90°，

∵∠AEC＝135°

∴∠AEF＝180°∠AEC＝45°＝∠EAF，

∴△AEF是等腰直角三角形，

∴AF＝EF＝AE，

∵，即：，

∴EF＋CE＝，即CF＝，

∵△ABC是等腰直角三角形，AB＝4

∴AC＝，

∴，

∴AE＝AF＝4，EF＝AF＝，

∴CE＝CFEF＝．