题目内容
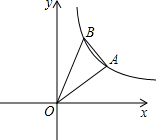 如图所示,Rt△OAB的A,B在反比例函数y=
如图所示,Rt△OAB的A,B在反比例函数y=6
| ||
| x |
A、9
| ||
B、6
| ||
C、12
| ||
D、2
|
考点:反比例函数综合题
专题:
分析:首先构造矩形,得出△ABC∽△OAE,则
=
=
,进而得出它们的比值,再假设出A点坐标,进而表示出B点坐标,再代入反比例函数解析式求出即可.
| AB |
| AO |
| BC |
| AE |
| AC |
| EO |
解答: 解:过点B作BF⊥y轴于点F,过点A作AE⊥x轴于点E,并延长FB,EA交于点C,
解:过点B作BF⊥y轴于点F,过点A作AE⊥x轴于点E,并延长FB,EA交于点C,
∵∠CFO=∠FOE=∠OEC=90°,
∴∠C=90°,
∴∠1+∠2=90°,
∵∠OAB=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
又∵∠OEA=∠C,
∴△ABC∽△OAE,
∴
=
=
,
∵∠BOA=30°,∠OAB=90°,
∴
=tan30°=
,
∵A,B在反比例函数y=
图象上的两点,
设A点坐标为:(a,
),
∴可得:FC=EO=a,AE=
,
∴
=
=
,
解得:BC=
,AC=
a,
∴BF=a-
,EC=
+
a,
∴B点坐标为:(a-
,
+
a),
∴(a-
)×(
+
a)=6
,
整理得出:a4-6a2-108=0,
解得:a2=3±3
(负数不合题意舍去),
∴a2=3+3
,
AO2=a2+(
)2=3+3
+
=6
.
故选:B.
 解:过点B作BF⊥y轴于点F,过点A作AE⊥x轴于点E,并延长FB,EA交于点C,
解:过点B作BF⊥y轴于点F,过点A作AE⊥x轴于点E,并延长FB,EA交于点C,∵∠CFO=∠FOE=∠OEC=90°,
∴∠C=90°,
∴∠1+∠2=90°,
∵∠OAB=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
又∵∠OEA=∠C,
∴△ABC∽△OAE,
∴
| AB |
| AO |
| BC |
| AE |
| AC |
| EO |
∵∠BOA=30°,∠OAB=90°,
∴
| AB |
| AO |
| ||
| 3 |
∵A,B在反比例函数y=
6
| ||
| x |
设A点坐标为:(a,
6
| ||
| a |
∴可得:FC=EO=a,AE=
6
| ||
| a |
∴
| BC | ||||
|
| AC |
| a |
| ||
| 3 |
解得:BC=
| 6 |
| a |
| ||
| 3 |
∴BF=a-
| 6 |
| a |
6
| ||
| a |
| ||
| 3 |
∴B点坐标为:(a-
| 6 |
| a |
6
| ||
| a |
| ||
| 3 |
∴(a-
| 6 |
| a |
6
| ||
| a |
| ||
| 3 |
| 3 |
整理得出:a4-6a2-108=0,
解得:a2=3±3
| 13 |
∴a2=3+3
| 13 |
AO2=a2+(
6
| ||
| a |
| 13 |
| 108 | ||
3+3
|
| 13 |
故选:B.
点评:此题主要考查了反比例函数综合应用以及相似三角形的判定与性质等知识,根据A点坐标进而表示出B点坐标是解题关键.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 如图,若OA、OB是⊙O的半径,CB是⊙O的弦,∠AOB=64°,则∠ACB=( )
如图,若OA、OB是⊙O的半径,CB是⊙O的弦,∠AOB=64°,则∠ACB=( )| A、16° | B、58° |
| C、32° | D、64° |
 如图,长方形纸片ABCD中,AD=9,AB=3,将其折叠,使其点D与B重合,折痕为EF,则DE和EF长分别为( )
如图,长方形纸片ABCD中,AD=9,AB=3,将其折叠,使其点D与B重合,折痕为EF,则DE和EF长分别为( )A、4,
| ||
B、4,2
| ||
C、5,
| ||
D、5,2
|
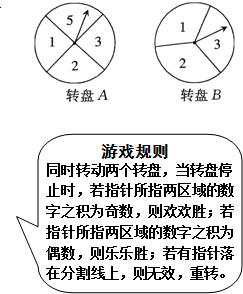 如图,把圆形转盘A平均4等份、圆形转盘B平均3等份,并在每一个小区域内标上数字.欢欢、乐乐两个人玩转盘戏,
如图,把圆形转盘A平均4等份、圆形转盘B平均3等份,并在每一个小区域内标上数字.欢欢、乐乐两个人玩转盘戏,