题目内容
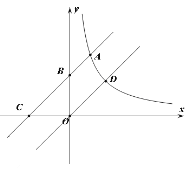
【题目】直线y=kx与反比例函数y=![]() (x>0)的图象相交点D(
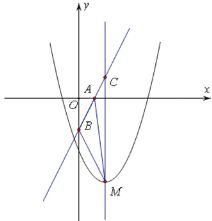
(x>0)的图象相交点D(![]() ,m),将直线y=kx向上平移b个单位长度与反比例函数的图象交于点A,与y轴交于点B,与x轴交于点C,且
,m),将直线y=kx向上平移b个单位长度与反比例函数的图象交于点A,与y轴交于点B,与x轴交于点C,且![]() ,求平移后的直线的表达式.
,求平移后的直线的表达式.
【答案】y=x+2
【解析】
过点A作AE⊥x轴于点E,先将点D(![]() ,m)代入y=
,m)代入y=![]() 得D(
得D(![]() ,
,![]() ),再代入y=kx得y=x,设平移后的直线的表达式为y=x+b,先证出△COB∽△CEA,根据相似三角形的性质得出对应边成比例,由
),再代入y=kx得y=x,设平移后的直线的表达式为y=x+b,先证出△COB∽△CEA,根据相似三角形的性质得出对应边成比例,由![]() 可推出AE=
可推出AE=![]() ,OE=
,OE=![]() ,即点A的坐标为
,即点A的坐标为![]() ,代入反比例函数
,代入反比例函数![]() 求得b的值,即可得平移后的直线的表达式.
求得b的值,即可得平移后的直线的表达式.
解:将点D(![]() ,m)代入y=
,m)代入y=![]() 得
得![]() ,∴
,∴![]()
把 D(![]() ,
,![]() )代入y=kx得k=1
)代入y=kx得k=1
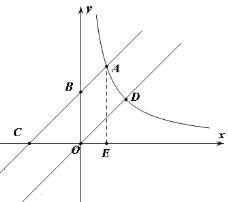
∴平移后的直线表达式为y=x+b
过点A作AE⊥x轴于点E,如图所示
∵AE⊥x轴,BO⊥x轴
∴AE∥BO
∴△COB∽△CEA
∴![]()
∵![]()
∴![]()
∵OB=b, ∴AE=![]()
根据题意得,点C的坐标为(-b,0) ∴CO=b,
∴![]() ∴CE=
∴CE=![]() OE=
OE=![]()
∴点A的坐标为(![]() ,
,![]() )
)
把A(![]() ,
,![]() )代入y=
)代入y=![]() 得
得![]() ,∴b=2
,∴b=2
∴平移后的直线表达式为y=x+2.
故答案为:y=x+2.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目