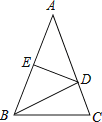Question

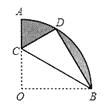
【题目】如图，在扇形OAB中，∠AOB=90°，半径OA=6．将扇形OAB沿过点B的直线折叠．点O恰好落在弧AB上点D处，折痕交OA于点C，求整个阴影部分的周长和面积．

Answer 1

【答案】12+3π；9π﹣12．

【解析】

解：连接OD．

根据折叠的性质，CD＝CO，BD＝BO，∠DBC＝∠OBC，

∴OB＝OD＝BD，即△OBD是等边三角形，

∴∠DBO＝60°，

∴∠CBO＝30°，

∵∠AOB＝90°，

∴OC＝OBtan∠CBO＝6×＝，

∴S△BDC＝S△OBC＝×OB×OC＝×6×＝，S扇形AOB＝，，

∴整个阴影部分的周长为：AC＋CD＋BD＋＝OA＋OB＋＝6＋6＋3π＝12＋3π；

整个阴影部分的面积为：S扇形AOBS△BDCS△OBC＝9π＝9π．