题目内容
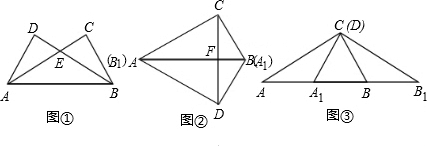
将两块大小一样含30°角的直角三角板叠放在一起,使得它们的斜边AB重合,直角边不重合,已知AB=8,AC与BD相交于点E,连接CD.

(1)如图①,若以AB所在直线为x轴,过A垂直于AB的直线为y轴建立平面直角坐标系,请你求出过A、B、C、D四点的抛物线的解析式;
(2)如图②,保持△ABD不动,将△ABC向x轴的正方向平移到△FGH的位置,FH与BD相交于点P,设AF=x,△FBP面积为y,求y与x之间的函数关系式.
分析:(1)利用有一角是30°的直角三角形的特性和勾股定理,求出A、B、C、D四点的坐标,利用A、B两点设出两点式解析式,代入C点求出,再代入D点验证,也可代入D点求出,用C点验证;
(2)作PM⊥AB,进一步利用有一角是30°的直角三角形的特性和勾股定理,用x表示出BF,再利用△HFG∽△MFP,用x表示出PM,最后运用三角形的面积求得.
(2)作PM⊥AB,进一步利用有一角是30°的直角三角形的特性和勾股定理,用x表示出BF,再利用△HFG∽△MFP,用x表示出PM,最后运用三角形的面积求得.
解答:解:(1)∵在Rt△ABC和Rt△ABD中,∠BAC=∠DBA=30°,AB=8,
∴A、B、C、D四点的坐标分别是:(0,0)、(8,0)、(6,2
)、(2,2
),
设:过A、B、C、D四点的抛物线的解析式为:y=a(x-x1)(x-x2),
∵A、B两点坐标为(0,0)、(8,0),
∴解析式为:y=a(x-0)(x-8)=ax(x-8),
∵D点的坐标是:(2,2
),
∴代入解析式得:2
=2a(2-8),
解得a=-
,
∴解析式为:y=-
x2+
x,
∵C点坐标是(6,2
),
把x=6代入解析式得:y=-6
+8
=2
,
∴C点在过A、B、D三点的抛物线上,
∴过A、B、C、D四点的抛物线的解析式是y=-
x2+
x.
(2)如图,
过点P做PM⊥AB垂足为M,
∴∠PMF=90°
在△FHG中,∠GHF=90°,∠GFH=30°,FG=8,
∴HG=4,
∴根据勾股定理得:FH=4
,
∵∠PMF=∠GHF=90°,∠HFG=∠MFP=30°,
∴△HFG∽△MFP,
∴
=
,
∵∠PFM=∠PBM=30°,
∴PF=PB,
∵PM⊥AB,
∴FM=
FB,
∵AF=x,AB=8,
∴FB=8-x,
∴FM=
,
由
=
可知,
.MP=
=
=
,
∴y=
(8-x)×
,
即:y=
x2-
x+
∴y与x的函数关系式为:y=
x2-
x+
.
∴A、B、C、D四点的坐标分别是:(0,0)、(8,0)、(6,2
| 3 |
| 3 |
设:过A、B、C、D四点的抛物线的解析式为:y=a(x-x1)(x-x2),
∵A、B两点坐标为(0,0)、(8,0),
∴解析式为:y=a(x-0)(x-8)=ax(x-8),
∵D点的坐标是:(2,2
| 3 |
∴代入解析式得:2
| 3 |
解得a=-
| ||
| 6 |
∴解析式为:y=-
| ||
| 6 |
4
| ||
| 3 |
∵C点坐标是(6,2
| 3 |
把x=6代入解析式得:y=-6
| 3 |
| 3 |
| 3 |
∴C点在过A、B、D三点的抛物线上,
∴过A、B、C、D四点的抛物线的解析式是y=-
| ||
| 6 |
4
| ||
| 3 |
(2)如图,
过点P做PM⊥AB垂足为M,
∴∠PMF=90°
在△FHG中,∠GHF=90°,∠GFH=30°,FG=8,
∴HG=4,
∴根据勾股定理得:FH=4
| 3 |
∵∠PMF=∠GHF=90°,∠HFG=∠MFP=30°,
∴△HFG∽△MFP,

∴
| MP |
| HG |
| FM |
| FH |
∵∠PFM=∠PBM=30°,
∴PF=PB,
∵PM⊥AB,
∴FM=
| 1 |
| 2 |
∵AF=x,AB=8,
∴FB=8-x,
∴FM=
| 8-x |
| 2 |
由
| MP |
| HG |
| FM |
| FH |
.MP=
4×
| ||
4
|
| 8-x | ||
2
|
8
| ||||
| 6 |
∴y=
| 1 |
| 2 |
8
| ||||
| 6 |
即:y=
| ||
| 12 |
4
| ||
| 3 |
16
| ||
| 3 |
∴y与x的函数关系式为:y=
| ||
| 12 |
4
| ||
| 3 |
16
| ||
| 3 |
点评:本题考查了二次函数解析式的确定、图形面积的求法、勾股定理、相似三角形的判定和性质等知识点.

练习册系列答案
相关题目
 C=AD=4,AC与BD相交于点E,连接CD.
C=AD=4,AC与BD相交于点E,连接CD.
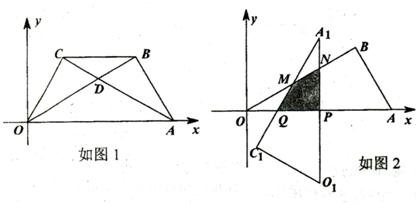
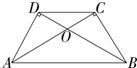 将两块大小一样含30°角的直角三角板如图叠放在一起,使它们的斜边AB重合,直角边不重合,当AB=8cm时,则两个直角顶点C、D的距离为
将两块大小一样含30°角的直角三角板如图叠放在一起,使它们的斜边AB重合,直角边不重合,当AB=8cm时,则两个直角顶点C、D的距离为