Question

如图，AB为⊙O的直径，AB=4，点C在⊙O上， CF⊥OC，且CF=BF.

（1）证明BF是⊙O的切线;
（2）设AC与BF的延长线交于点M，若MC=6，求∠MCF的大小.

Answer 1

证明：连接OF.
（1） ∵ CF⊥OC,
∴ ∠FCO=90°.
∵ OC=OB，
∴ ∠BCO=∠CBO.
∵ FC=FB，
∴ ∠FCB=∠FBC.        …………………………..1分
∴ ∠BCO+∠FCB =∠CBO+∠FBC.
即 ∠FBO=∠FCO=90°.
∴ OB⊥BF.
∵ OB是⊙O的半径,
∴ BF是⊙O的切线.…………………………..2分
（2）  ∵ ∠FBO=∠FCO=90°，
∴ ∠MCF+∠ACO =90°，∠M+∠A =90°.
∵ OA=OC，
∴ ∠ACO=∠A.
∴ ∠FCM=∠M.  ………………………3分
易证△ACB∽△ABM,
∴ .
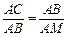∵ AB=4，MC=6，
∴ AC="2.   " …………………………………………..4分
∴ AM=8，BM==.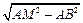
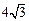∴cos∠MC F =" cosM" ==.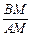
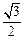∴ ∠MCF=30°. ……………………………………..5分

解析