Question

已知：如图△ABC中，∠BAC=45°，AD是高．
（1）请你分别画△ABD关于AB对称的△ABE和△ACD关于AC对称的△ACF；
（2）若再延长EB、FC交于G，你能判断出四边形AEGF是什么四边形吗？试说明理由．

Answer 1

【答案】分析：（1）作D关于AB的对称点E，连接AE、BE，即可得△ABE，作△ACF同上．
（2）判断出四边形AEGF是正方形．由作图过程和题意易得三角是直角，且AE=AF．即可证明．
解答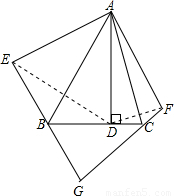：解：（1）如图．（4分）

（2）正方形（6分）
证明：由作图过程易得△ABD≌△ABE，△ADC≌△AFC
∴∠AEB=∠ADC=90°，∠AFC=∠ADC=90°，∠BAE=∠BAD，∠DAC=∠FAC，AE=AD=AF
∵∠BAC=45°
∴∠EAF=2∠BAC=90°
∴四边形AEGF是矩形（有三角都是直角的四边形是矩形）
∵AE=AF
∴四边形AEGF是正方形（邻边相等的矩形是正方形．）
（10分）
点评：此题考查轴对称图形的作法、动手操作、正方形的判定．