题目内容
图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:
(1) 在图1中,请直接写出∠A+∠D与∠B+∠C之间的数量关系为 ;
(2)仔细观察,在图2中“8字形”的个数: 个;
(3)图2中,当∠D=50度,∠B=40度时,求∠P的度数。
(4)图2中∠D和∠B为任意角时,其他条件不变,试问∠P与
∠D、∠B之间存在着怎样的数量关系。(直接写出结果,不必证明)。


解:(1) ∠A+∠D=∠C+∠B …………………………… 2分
(2) 3 个 ………………………………………… 4分
(3)解:∠DAP+∠D=∠P+∠DCP ①
![]() ∠PCB+∠B=∠PAB+∠P ② …………… 6分
∠PCB+∠B=∠PAB+∠P ② …………… 6分
∵∠DAB和∠BCD的平分线AP和CP相交于点P
∴∠DAP=∠PAB,∠DCP= ∠PCB ………………… 7分
+②得:∠DAP+∠D+∠PCB+∠B =∠P+∠DCP+∠PAB+∠P………… 9分
又∵∠D=50度,∠B=40度 ∴50°+40°=2∠P
∴∠P=45°…………………………………………… 10分
(4)关系:2∠ P=∠D+∠B ………………………… 12分

练习册系列答案
相关题目
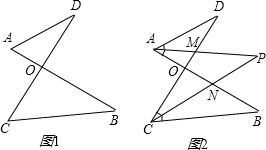


 如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.其中正确结论是( )
如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.其中正确结论是( )