题目内容
 如图,△ABC是等边三角形,P是∠ABC的平分线BD上一点,PE⊥AB于点E,线段BP的垂直平分线交BC于点F,垂足为点Q.若BF=2,则PE的长为
如图,△ABC是等边三角形,P是∠ABC的平分线BD上一点,PE⊥AB于点E,线段BP的垂直平分线交BC于点F,垂足为点Q.若BF=2,则PE的长为
- A.2
- B.2

- C.

- D.3
C
分析:先根据△ABC是等边三角形P是∠ABC的平分线可知∠EBP=∠QBF=30°,再根据BF=2,FQ⊥BP可得出BQ的长,再由BP=2BQ可求出BP的长,在Rt△BEF中,根据∠EBP=30°即可求出PE的长.
解答:∵△ABC是等边三角形P是∠ABC的平分线,
∴∠EBP=∠QBF=30°,
∵BF=2,QF为线段BP的垂直平分线,
∴∠FQB=90°,
∴BQ=BF•cos30°=2× =
= ,
,
∴BP=2BQ=2 ,
,
在Rt△BEF中,
∵∠EBP=30°,
∴PE= BP=
BP= .
.
故选C.
点评:本题考查的是等边三角形的性质、角平分线的性质及直角三角形的性质,熟知等边三角形的三个内角都是60°是解答此题的关键.
分析:先根据△ABC是等边三角形P是∠ABC的平分线可知∠EBP=∠QBF=30°,再根据BF=2,FQ⊥BP可得出BQ的长,再由BP=2BQ可求出BP的长,在Rt△BEF中,根据∠EBP=30°即可求出PE的长.
解答:∵△ABC是等边三角形P是∠ABC的平分线,
∴∠EBP=∠QBF=30°,
∵BF=2,QF为线段BP的垂直平分线,
∴∠FQB=90°,
∴BQ=BF•cos30°=2×
 =
= ,
,∴BP=2BQ=2
 ,
,在Rt△BEF中,
∵∠EBP=30°,
∴PE=
 BP=
BP= .
.故选C.
点评:本题考查的是等边三角形的性质、角平分线的性质及直角三角形的性质,熟知等边三角形的三个内角都是60°是解答此题的关键.

练习册系列答案
相关题目
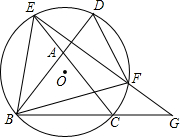 ∥AC,EF的延长线交BC的延长线于点G.
∥AC,EF的延长线交BC的延长线于点G. 9、如图,△ABC是等边三角形,过AB边上一点D作BC的平行线交AC于E,则△ADE的三个内角
9、如图,△ABC是等边三角形,过AB边上一点D作BC的平行线交AC于E,则△ADE的三个内角 如图,△ABC是等边三角形,AB=4cm,则BC边上的高AD等于
如图,△ABC是等边三角形,AB=4cm,则BC边上的高AD等于 如图,△ABC是等边三角形,D为BC边上的点,∠BAD=15°,将△ABD绕点A点逆时针方向旋转后到达△ACE的位置,那么旋转角的度数是
如图,△ABC是等边三角形,D为BC边上的点,∠BAD=15°,将△ABD绕点A点逆时针方向旋转后到达△ACE的位置,那么旋转角的度数是 如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.
如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.