题目内容
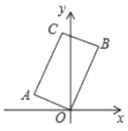
【题目】如图,直线![]() :
:![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,在
两点,在![]() 轴上有一点
轴上有一点![]() ,动点
,动点![]() 从
从![]() 点开始以每秒1个单位的速度匀速沿
点开始以每秒1个单位的速度匀速沿![]() 轴向左移动.
轴向左移动.

(1)点![]() 的坐标:________;点
的坐标:________;点![]() 的坐标:________;
的坐标:________;
(2)求![]() 的面积
的面积![]() 与
与![]() 的移动时间
的移动时间![]() 之间的函数解析式;
之间的函数解析式;
(3)在![]() 轴右边,当
轴右边,当![]() 为何值时,
为何值时,![]() ,求出此时点
,求出此时点![]() 的坐标;
的坐标;
(4)在(3)的条件下,若点![]() 是线段
是线段![]() 上一点,连接
上一点,连接![]() ,
,![]() 沿
沿![]() 折叠,点
折叠,点![]() 恰好落在
恰好落在![]() 轴上的点
轴上的点![]() 处,求点
处,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]()
【解析】
(1)在![]() 中,分别令y=0和x=0,则可求得A、B的坐标;
中,分别令y=0和x=0,则可求得A、B的坐标;
(2)利用t可表示出OM,则可表示出S,注意分M在y轴右侧和左侧两种情况;
(3)由全等三角形的性质可得OM=OB=2,则可求得M点的坐标; .
(4)由勾股定理可得:![]() ,折叠可知;
,折叠可知;![]() ,可得:
,可得:![]() ,故
,故![]() ,
,![]() ,设
,设![]() ,则
,则![]() ,在
,在![]() 中,根据勾股定理可列得方程
中,根据勾股定理可列得方程![]() ,即可求出答案.
,即可求出答案.
解:(1)在![]() 中, 令y=0可求得x=4, 令x=0可求得y=2,
中, 令y=0可求得x=4, 令x=0可求得y=2,
∴A(4,0),B(0,2)
故答案为:(4,0) ;(0,2)
(2)由题题意可知AM=t,
①当点M在y轴右边时,OM=OA-AM=4-t,
∵N (0,4)
∴ON=4,
∴![]() ,
,
即![]() ;
;
当点![]() 在
在![]() 轴左边时,则OM=AM-OA=t-4,
轴左边时,则OM=AM-OA=t-4,
∴![]() ,
,
即![]() .
.
∴![]()
(3)若![]() ,则有
,则有![]() ,
,
∴![]() .
.
(4)由(3)得,![]() ,
,![]() ,
,
∴![]() .
.
∵![]() 沿
沿![]() 折叠后与
折叠后与![]() 重合,
重合,
∴![]() ,
,
∴![]() ,
,
∴此时点![]() 在
在![]() 轴的负半轴上,
轴的负半轴上,![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,
解得![]() ,
,
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目