题目内容
如图,将边长为4的正方形纸片,置于平面直角坐标系内,顶点A在坐标原点,AB在x轴正方向上,E、F分别是A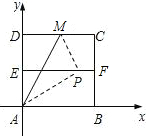 D、BC的中点,M在DC上,将△ADM沿折痕AM折叠,使点D折叠后恰好落在EF上的P点处.
D、BC的中点,M在DC上,将△ADM沿折痕AM折叠,使点D折叠后恰好落在EF上的P点处.(1)求点M、P的坐标;
(2)求折痕AM所在直线的解析式;
(3)设点H为直线AM上的点,是否存在这样的点H,使得以H、A、P为顶点的三角形为等腰三角形?若存在,请直接写出点H的坐标;若不存在,请说明理由.
分析:(1)根据勾股定理求出EP的值然后可得点P的坐标.作MN⊥EF.设DM=x,PN=2
-x求出x的值.
(2)设折痕AM所在直线的解析式为y=kx,把点M的坐标代入可得k值,然后可求解析式.
(3)根据线段的垂直平分线定理可解.
| 3 |
(2)设折痕AM所在直线的解析式为y=kx,把点M的坐标代入可得k值,然后可求解析式.
(3)根据线段的垂直平分线定理可解.
解答: 解:(1)依据题意
解:(1)依据题意
∵AP=AD=4,AE=2,
∴EP=
=
=2
.
∴P点坐标为(2
,2). (3分)
设DM=x,则MP=x,过M作MN⊥EF,垂足为N,
则MN=2,PN=2
-x.
在Rt△MNP中,22+(2
-x)2=x2
解之得:x=
.
∴M点坐标为(
,4). (6分)
(2)设折痕AM所在直线的解析式为y=kx(k≠0),则4=
k,
k=
.
∴折痕AM所在直线的解析式为y=
x. (8分)
(3)存在;H1(-2,-2
);H2(
,2);H3(2,2
);H4(2
,6). (14分)
 解:(1)依据题意
解:(1)依据题意∵AP=AD=4,AE=2,
∴EP=
| AP2-AE2 |
| 16-4 |
| 3 |
∴P点坐标为(2
| 3 |
设DM=x,则MP=x,过M作MN⊥EF,垂足为N,
则MN=2,PN=2
| 3 |
在Rt△MNP中,22+(2
| 3 |
解之得:x=
4
| ||
| 3 |
∴M点坐标为(
4
| ||
| 3 |
(2)设折痕AM所在直线的解析式为y=kx(k≠0),则4=
4
| ||
| 3 |
k=
| 3 |
∴折痕AM所在直线的解析式为y=
| 3 |
(3)存在;H1(-2,-2
| 3 |
2
| ||
| 3 |
| 3 |
| 3 |
点评:【命题意图】此题综合考查了一次函数的性质,解直角三角形、线段的垂直平分线等知识.难度中上.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
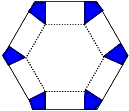 如图,将边长为6cm的正六边形纸板的六个角各剪切去一个全等的四边形,再沿虚线折起,做成一个无盖直六棱柱纸盒,使侧面积等于底面积,被剪去的六个四边形的面积和为
如图,将边长为6cm的正六边形纸板的六个角各剪切去一个全等的四边形,再沿虚线折起,做成一个无盖直六棱柱纸盒,使侧面积等于底面积,被剪去的六个四边形的面积和为 (2013•丰南区一模)如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为
(2013•丰南区一模)如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为