题目内容

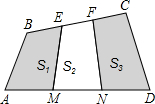如图所示，在四边形ABCD中，AM=MN=ND，BE=EF=FC，四边形ABEM，MEFN，NFCD的面积分别记为S₁，S₂和S₃，求 $数学公式$ =？
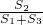（提示：连接AE、EN、NC和AC）

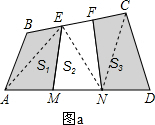解：如图a所示：连接AE、EN和NC，设四边形AECN的面积为S，
∵AM=MN=ND，BE=EF=FC，
∴S_△AEM=S_△MEN，S_△CNF=S_△EFN，
上面两个式子相加得S_△AEM+S_△CNF=S₂
并且四边形AECN的面积S=2S₂，即：S₂= $\text{[math]}$ S，S_△AEM+S_△CNF= $\text{[math]}$ S．
连接AC，如图b所示：
∵AM=MN=ND，BE=EF=FC，
∴CE=2BE，NA=2DN，
∴S_△ABE= $\text{[math]}$ S_△AEC，S_△CDN= $\text{[math]}$ S_△CNA，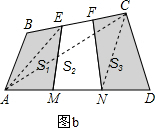

上面两个式子相加得S_△ABE+S_△CDN= $\text{[math]}$ ×四边形AECN的面积= $\text{[math]}$ S，
所以，S_△AEM+S_△CNF+S_△ABE+S_△CDN= $\text{[math]}$ S+ $\text{[math]}$ S=S，
因此S₁+S₃=S， $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ．
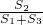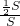答： $\text{[math]}$ = $\text{[math]}$ ．
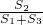分析：分别连接AE、EN和NC、AC，要求S₂与S₁+S₃之间的关系，可先设四边形AECN的面积为S，根据三角形的面积公式分别求出S₁+S₃、S₂与四边形AECN的面积为S之间的关系，求出 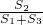$\text{[math]}$ 即可．
点评：本题主要考查了灵活运用三角形的面积公式，分别求出各个量与中间量得关系，分别用中间量表示各个量，代入所求式子求值的方法，关键在于设出合适的中间量．