题目内容
设a、b、c、a+b-c、a+c-b、b+c-a、a+b+c是七个两两不同的质数，且a、b、c中有两数之和是800．设d是这七个质数中最大数与最小数的差，求d的最大可能值．
分析：不妨设a＜b＜c，显然a+b+c最大，a+b-c最小，所以d=2c，只需求c的最大值即可．
解答：解：设a＜b＜c，显然a+b+c最大，a+b-c最小，所以d=2c．
∵a+b-c＞0，∴c＜a+b，c＜a+c，c＜b+c，
∴c＜800，小于800的质数从小到大依次为797，787，…
若c=797，a+b=800，a+b-c=3，a+b+c=1597，令a=13，b=787，a+c-b=23，b+c-a=1571，不难验证都为质数，所以dmax=2×797=1594．
∵a+b-c＞0，∴c＜a+b，c＜a+c，c＜b+c，
∴c＜800，小于800的质数从小到大依次为797，787，…
若c=797，a+b=800，a+b-c=3，a+b+c=1597，令a=13，b=787，a+c-b=23，b+c-a=1571，不难验证都为质数，所以dmax=2×797=1594．
点评：本题主要考查学生的转换思想，此题将求d的最大值转化成求c的最大值就可解决了．
练习册系列答案
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
八年级某班级部分同学去植树，若每人平均植树7棵，还剩9棵，若每人平均植树9棵，则有1名同学植树的棵数不到8棵．若设同学人数为x人，下列各项能准确的求出同学人数与种植的树木的数量的是（ ）
| A、7x+9-9（x-1）＞0 | |||||
| B、7x+9-9（x-1）＜8 | |||||
C、
| |||||
D、
|
已知⊙O1的半径为R，周长为C．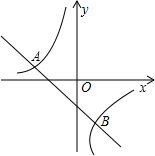
如图，若反比例函数y=-