Question

如图，将两个完全一样含有30°角的直角三角板如图摆放（点D、B、C在一条直线上），∠A与∠D为30°角，∠ABC与∠DCE为直角．
（1）求证：AN•NE=CN•MN；
（2）连结AD、AE，若BC=6cm，求四边形ADCE的面积．

Answer 1

（1）证明：如图，∵∠ABD=∠DCE=90°，
∴AB∥CE，即AM∥EC，
∴△AMN∽△CEN，
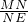∴=，则AN•NE=CN•MN；

（2）如图，在直角△ABC中，∠ABC=90°，BC=6cm，∠A=30°，
∴AC=2BC=12cm，则根据勾股定理得到：AB==6cm．
又∵CD=AB，
∴BD=AB-BC=（6-6）cm，
∴S_{四边形ADCE}=S_△ADB+S_梯形ABCD=AB•BD+（EC+AB）•BC=×6+×（6+6）×6=21+18（cm²）．
分析：（1）通过证明△AMN∽△CEN得到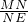：=，则由比例的性质证得结论；
（2）依题意知EC=BC=6cm．则由“30度角所对的直角边是斜边的一半”和勾股定理易求DC、AB的长度．从而求得BD=CD-BC，则由直角三角形的面积公式和直角梯形的面积公式求得S_{四边形ADCE}=S_△ADB+S_梯形ABCD．
点评：本题考查了相似三角形的判定与性质．解答（2）题时，利用了“割补法”求得的四边形ADCE的面积．