Question

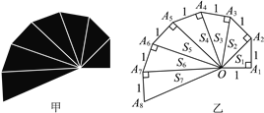
【题目】甲是第七届国际数学教育大会的会徽，会徽的主体图案是由图乙中的一连串直角三角形演化而成的，其中OA1＝A1A2＝A2A3＝…＝A7A8＝1．

细心观察图形，认真分析下列各式，然后解答问题：

()2＋1＝2，S1＝；()2＋1＝3，S2＝；（）２＋1＝4，S3＝；…．

（1）请用含有n(n是正整数)的等式表示上述变化规律，并计算出OA10的长；

（2）求出的值．

Answer 1

【答案】（1）含有n(n是正整数)的等式表示上述变化规律为：，OA10的长为；（2）

【解析】

（1）根据勾股定理分别求出OA22、OA32，OA42及OA2、OA3、OA4得到OAn2及OAn对应的S值，再计算得到OA10；

（2）由（1）知，分别求出S1、S2、S3、、S10，将结果代入代数式计算即可.

（1）∵OA1=1=，OA1＝A1A2＝A2A3＝…＝A7A8＝1，

∴OA22==1+1=2，

∴OA2=，，

∵OA32==()2＋1＝3，

∴，，

∵OA42==（）２＋1＝4，

∴OA4=2， ，

，

∴，，

∴OA102==10，

∴OA10= ，

∴含有n(n是正整数)的等式表示上述变化规律为：，OA10的长为；

（2）由（1）知：，

∴， ， ，，，

∴==.