题目内容
如图,直线y=x-3交坐标轴于A、B两点,交双曲线y=
于点D(D在第一象限),过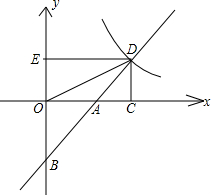 D作两坐标轴的垂线DC、DE,连接OD.
D作两坐标轴的垂线DC、DE,连接OD.
(1)在不对图形作任何变动的情况下,直接写出图形中的三个等腰直角三角形;
(2)求证:AD•BD=4;
(3)将直线AB沿x轴平移,是否存在直线AB,使得四边形OBCD为平行四边形?若存在,求直线的解析式;若不存在,说明理由.
| 2 | x |
 D作两坐标轴的垂线DC、DE,连接OD.
D作两坐标轴的垂线DC、DE,连接OD.(1)在不对图形作任何变动的情况下,直接写出图形中的三个等腰直角三角形;
(2)求证:AD•BD=4;
(3)将直线AB沿x轴平移,是否存在直线AB,使得四边形OBCD为平行四边形?若存在,求直线的解析式;若不存在,说明理由.
分析:(1)直线y=x-3与x轴所夹的锐角为45°,分析可发现三个等腰直角三角形;
(2)由等腰直角三角形的性质可知,AD=
CD,BD=
DE,由于CD•DE=xy=2,由此可证AD•BD=4;
(3)当点A为OC的中点时,四边形OBCD为平行四边形,设平移后的直线解析式为y=x-b,则OA=OB=AC=CD=b,D(2b,b),将D点坐标代入y=
中求b.
(2)由等腰直角三角形的性质可知,AD=
| 2 |
| 2 |
(3)当点A为OC的中点时,四边形OBCD为平行四边形,设平移后的直线解析式为y=x-b,则OA=OB=AC=CD=b,D(2b,b),将D点坐标代入y=
| 2 |
| x |
解答:解:(1)Rt△BOA,Rt△BED,Rt△ACD;
(2)∵△BED,△ACD为等腰直角三角形,
∴AD=
CD,BD=
DE,
∴AD•BD=
CD•
DE=2xy=2×2=4;
(3)存在.当点A为OC的中点时,四边形OBCD为平行四边形.理由如下:
设平移后的直线解析式为y=x-b,
则OA=OB=AC=CD=b,D(2b,b),
将D点坐标代入y=
中,得2b2=2,解得b=1(舍去负值),
所以,直线解析式为y=x-1.
(2)∵△BED,△ACD为等腰直角三角形,
∴AD=
| 2 |
| 2 |
∴AD•BD=
| 2 |
| 2 |
(3)存在.当点A为OC的中点时,四边形OBCD为平行四边形.理由如下:
设平移后的直线解析式为y=x-b,
则OA=OB=AC=CD=b,D(2b,b),
将D点坐标代入y=
| 2 |
| x |
所以,直线解析式为y=x-1.
点评:本题考查了反比例函数的综合运用.关键是掌握直线y=x-3与x轴所夹锐角为45°,反比例函数图象上点的横纵坐标的积为常数.

练习册系列答案
相关题目

 13、如图,直线a、b都与直线c相交,给出下列条件:(1)∠l=∠2;(2)∠3=∠6;(3)∠4+∠7=180°;(4)∠5+∠8=180°,其中能判断a∥b的是( )
13、如图,直线a、b都与直线c相交,给出下列条件:(1)∠l=∠2;(2)∠3=∠6;(3)∠4+∠7=180°;(4)∠5+∠8=180°,其中能判断a∥b的是( ) 4、如图,直线AB、CD相交于点E,EF⊥AB于E,若∠CEF=59°,则∠AED的度数为( )
4、如图,直线AB、CD相交于点E,EF⊥AB于E,若∠CEF=59°,则∠AED的度数为( ) 如图,直线y=6-x交x轴、y轴于A、B两点,P是反比例函数
如图,直线y=6-x交x轴、y轴于A、B两点,P是反比例函数 17、如图,直线a∥c,b∥c,直线d与直线a、b、c相交,已知∠1=60°,求∠2、∠3的度数(可在图中用数字表示角).
17、如图,直线a∥c,b∥c,直线d与直线a、b、c相交,已知∠1=60°,求∠2、∠3的度数(可在图中用数字表示角).