题目内容
 如图,把边长是3的正方形等分成9个小正方形,在有阴影的两个小正方形ABCD和EFGH内(包括边界)分别取两个动点P、R,与已有格点Q(每个小正方形的顶点叫格点)构成三角形,则当△PQR的面积取得最大值2时,点P和点R所在位置是
如图,把边长是3的正方形等分成9个小正方形,在有阴影的两个小正方形ABCD和EFGH内(包括边界)分别取两个动点P、R,与已有格点Q(每个小正方形的顶点叫格点)构成三角形,则当△PQR的面积取得最大值2时,点P和点R所在位置是分析:当△PQR的面积取得最大值2时,可知当三角形的底边长为2,高为2时,面积最大,故点P在A处,点R在F处或点P在B处,点R在G处时,符合题意.
解答:解:


①当点P在A处,点R在F处时,S△AQF=
AQ•GQ=
×2×2=2;
②当点P在B处,点R在G处时,S△BQG=
GQ•AQ=
×2×2=2,
③点P在A,点R在G处时,S△AQG=
GQ•AQ=
×2×2=2.
故当点P在A处,点R在F处时,或是当点P在B处,点R在G处时,或点P在A,点R在G处时,△PQR的面积最大,且最大值是2.


①当点P在A处,点R在F处时,S△AQF=
| 1 |
| 2 |
| 1 |
| 2 |
②当点P在B处,点R在G处时,S△BQG=
| 1 |
| 2 |
| 1 |
| 2 |
③点P在A,点R在G处时,S△AQG=
| 1 |
| 2 |
| 1 |
| 2 |
故当点P在A处,点R在F处时,或是当点P在B处,点R在G处时,或点P在A,点R在G处时,△PQR的面积最大,且最大值是2.
点评:在解本题时要注意数形结合.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
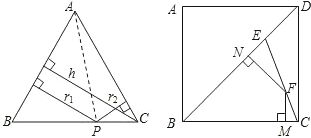
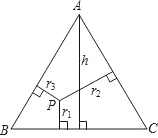






 AB•r1+
AB•r1+

 AB•r1+
AB•r1+ AC•r2=
AC•r2= AC•h,∴r1+r2=h(定值).
AC•h,∴r1+r2=h(定值).
