Question

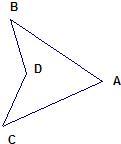27、附加题：如图，试说明：
①∠BDC＞∠A；
②∠BDC=∠B+∠C+∠A．
如果点D在线段BC的另一侧，结论会怎样？

Answer 1

分析：根据“三角形的一个外角大于任何一个和它不相邻的内角”来比较大小．
根据“三角形的外角等于与它不相邻的两个内角和”来求∠BDC=∠B+∠C+∠A．

解答：解：①延长BD交AC于E，则∠BDC＞∠DEC，而∠DEC＞∠A，所以∠BDC＞∠A；


②由∠BDC=∠C+∠DEC，而∠DEC=∠A+∠B，所以∠BDC=∠A+∠B+∠C．

点评：主要考查了三角形的内角和外角之间的关系：
（1）三角形的外角等于与它不相邻的两个内角和；
（2）三角形的一个外角大于任何一个和它不相邻的内．