Question

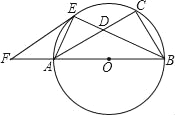
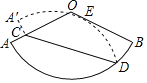
【题目】如图，已知扇形AOB的圆心角为120°，点C是半径OA上一点，点D是上一点．将扇形AOB沿CD对折，使得折叠后的图形恰好与半径OB相切于点E．若∠OCD＝45°，OC＝+1，则扇形AOB的半径长是（　　）

A. 2+B. 2+C. 2D.

Answer 1

【答案】B

【解析】

作O关于CD的对称点F，连接CF、EF，则EF为扇形AOB的半径，由折叠的性质得：∠FCD＝∠OCD＝45°，FC＝OC＝+1，得出△OCF是等腰直角三角形，得出∠COF＝45°，OF＝OC＝+，∠EOF＝∠AOB﹣∠COF＝75°，由切线的性质得出∠OEF＝90°，得出∠OFE＝15°，由三角函数即可得出结果．

作O关于CD的对称点F，连接CF、EF，如图1所示：

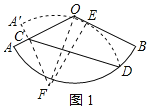
则EF为扇形AOB的半径，

由折叠的性质得：∠FCD＝∠OCD＝45°，FC＝OC＝+1，

∴∠OCF＝90°，

∴△OCF是等腰直角三角形，

∴∠COF＝45°，OF＝OC＝+，

∴∠EOF＝∠AOB﹣∠COF＝75°，

∵折叠后的图形恰好与半径OB相切于点E，

∴∠OEF＝90°，

∴∠OFE＝15°，

∵cos∠OFE＝cos15°＝，

如图2所示：

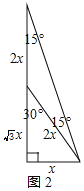
∴EF＝OF×cos15°＝（+）×＝2+；

故选：B．