题目内容
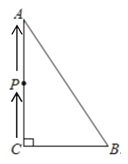
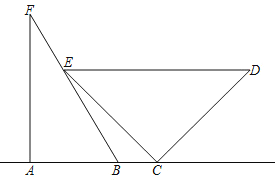
【题目】数学课上,静静将一幅三角板如图摆放,点![]() ,
,![]() ,
,![]() 三点共线,其中
三点共线,其中![]() ,
,![]() ,
,![]() ,且
,且![]() .
.
(1)若![]() ,
,![]() .求
.求![]() 的长.
的长.
(2)若![]() ,求
,求![]() 的长.
的长.
【答案】(1)![]() ;(2)2-
;(2)2-![]() .
.
【解析】
(1)在直角△AFB中,利用勾股定理求得AF的长度;
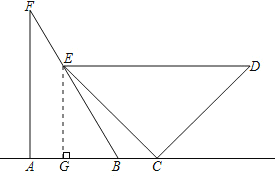
(2)如图,过点E作EG⊥AC于点G,构造等腰直角△EGC.在直角△EDC中,根据勾股定理求得EC的长度;然后在直角△EGC中,再次利用勾股定理求得GC的长度,在直角△EGB中,求得BG的长度,则BC=GC-GB.
(1)解:如图,直角△AFB中,∠FAB=90°,AB=2,BF=4.
由勾股定理知,AF=![]() ;
;
(2)解:如图,过点E作EG⊥AC于点G,则AF∥EG.
∵∠F=30°,
∴∠BEG=30°.
∴BG=![]() BE.
BE.
∵∠ECD=90°,∠D=45°,
∴∠DEC=∠D=45°.
∴EC=CD.
∴ED=![]() EC.
EC.
又ED=4,
∴EC=2![]() .
.
∵DE∥AC,
∴∠ECG=∠DEC=45°.
∴∠GEC=∠GCE=45°.
∴EG=CG.
∴EC=![]() GC,即2
GC,即2![]() =
=![]() GC.
GC.
∴GC=2.
在直角△BGE中,由勾股定理知BG2+EG2=BE2,即BG2+22=4BG2.
∴BG=![]() .
.
∴BC=GC-GB=2-![]() .
.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目