Question

如图，已知八边形ABCDEFGH中4个正方形的面积分别为25，144，48，121个平方单位，PR=13（单位），则该八边形的面积=________平方单位．

Answer 1

428+66
分析：由PR=13、PS=12、RS=5得出PS⊥SR，PQ⊥QR，求出四边形PQRS的面积，作QI⊥PS交于I，BJ⊥AP交AP的延长线于J，利用全等证出
QI=BJ，推出S_△APB+S_△EFR=S_{四边形PQRS}，再把各部分的面积相加即可得到答案．
解答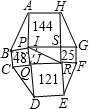：解：∵4个正方形的面积分别为25，144，48，121，
∴边长分别为：5、12、4、11，
∵PR=13、PS=12、RS=5，
∴PS⊥SR，PQ⊥QR，
∴S_{四边形PQRS}=（PS•SR+PQ•QR）=30+22，
显然S_△HSG+S_△CDQ=S_{四边形PQRS}，
如图作QI⊥PS交于I，BJ⊥AP交AP的延长线于J，
∵BP=PQ，∠BJP=∠QIP=90°，
∵∠APB+∠QPS=360°-90°-90°=180°，
∴∠QPS=∠BPJ，
∴Rt△PQI≌Rt△PBJ，
∴QI=BJ，
∴S_△APB=S_△PSQ，
同理S_△EFR=S_△QSR，
则S_△APB+S_△EFR=S_{四边形PQRS}，
故八边形的面积=3（30+22）+144+48+121+25，
=428+66．
故答案为：428+66．
点评：本题主要考查了面积与等积变换，全等三角形的性质和判定，三角形的面积，勾股定理的逆定理等知识点，正确求出各部分的面积是解此题的关键．题目较好但有一定难度．