题目内容
如图,直角三角形ABC中,∠ABC=90°,B(2,0),经过A、B、C三点的抛物线y=
x2-2x+k与y轴交于点A,与x轴的另一个交点为D.
(1)求此抛物线的解析式;
(2)⊙B是以点B为圆心,OB长为半径的圆,以点D为圆心的⊙D与直线BC相切,请你通过计算说明:⊙B与⊙D的位置关系;
(3)在直线AD下方的抛物线上是否存在一点P,使四边形APDC的面积最大?若存在,请你求出点P的坐标和四边形APDC面积的最大值;若不存在,请你说明理由.
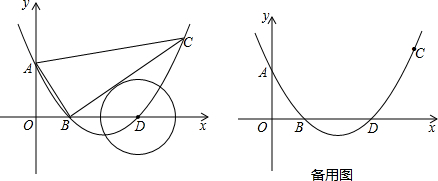
| 1 | 4 |
(1)求此抛物线的解析式;
(2)⊙B是以点B为圆心,OB长为半径的圆,以点D为圆心的⊙D与直线BC相切,请你通过计算说明:⊙B与⊙D的位置关系;
(3)在直线AD下方的抛物线上是否存在一点P,使四边形APDC的面积最大?若存在,请你求出点P的坐标和四边形APDC面积的最大值;若不存在,请你说明理由.
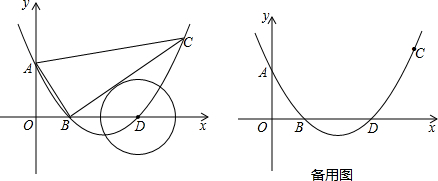
分析:(1)直接将点B的坐标代入抛物线的解析式中,即可确定待定系数的值.
(2)此题的关键是求出点D的坐标(由此得到BD的距离)以及⊙D的半径,首先由抛物线的解析式求出点D的坐标,再连接圆心D与切点,通过构建的相似三角形来解.然后通过比较两圆的半径以及BD的长来得到两圆的位置关系.
(3)由于∠ABC是直角,过点C作x轴的垂线,通过构建的相似三角形可以求出点C的坐标表达式,再代入抛物线的解析式中可确定点C的坐标,然后通过图形间的面积和差关系求出△ADC的面积;若△APDC的面积最大,那么△APD的面积最大(因为△ADC的面积是定值),可先求出直线AD的解析式,然后过点D作y轴的平行线,交直线AD于Q,在表达出点P、Q的坐标后,可得到线段PQ的表达式,以PQ为底,点A、D横坐标的差的绝对值为高,可求出△APD的面积,由此可得四边形APDC的面积与点P的横坐标函数关系式,根据函数的性质可求出四边形APDC的最大面积以及此时点P的坐标.
(2)此题的关键是求出点D的坐标(由此得到BD的距离)以及⊙D的半径,首先由抛物线的解析式求出点D的坐标,再连接圆心D与切点,通过构建的相似三角形来解.然后通过比较两圆的半径以及BD的长来得到两圆的位置关系.
(3)由于∠ABC是直角,过点C作x轴的垂线,通过构建的相似三角形可以求出点C的坐标表达式,再代入抛物线的解析式中可确定点C的坐标,然后通过图形间的面积和差关系求出△ADC的面积;若△APDC的面积最大,那么△APD的面积最大(因为△ADC的面积是定值),可先求出直线AD的解析式,然后过点D作y轴的平行线,交直线AD于Q,在表达出点P、Q的坐标后,可得到线段PQ的表达式,以PQ为底,点A、D横坐标的差的绝对值为高,可求出△APD的面积,由此可得四边形APDC的面积与点P的横坐标函数关系式,根据函数的性质可求出四边形APDC的最大面积以及此时点P的坐标.
解答:解:(1)∵抛物线y=
x2-2x+k经过点B(2,0),
∴
×4-2×2+k=0,k=3;
故抛物线的解析式:y=
x2-2x+3.
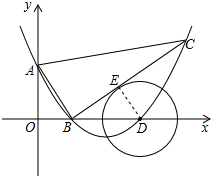 (2)由(1)的抛物线解析式知:A(0,3)、D(6,0);
(2)由(1)的抛物线解析式知:A(0,3)、D(6,0);
设⊙D与直线BC的切点为E,连接DE,则 DE⊥BE;
∵∠ABC=90°,
∴∠ABO=∠BDE=90°-∠DBE,又∠AOB=∠BED=90°,
∴△AOB∽△BED,有:
=
,即
=
,r=
≈2.2;
∴2.2-2<BD<2.2+2,即rD-rB<BD<rD+rB
∴⊙B与⊙D的位置关系为相交.
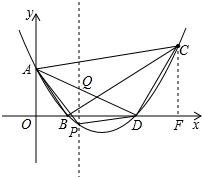 (3)过点C作CF⊥x轴于点F,设点C(x,
(3)过点C作CF⊥x轴于点F,设点C(x,
x2-2x+3),则 CF=
x2-2x+3,BF=x-2;
同(2)可证得:Rt△AOB∽Rt△BFC,有:
=
,即
=
解得:x1=2(舍)、x2=
;
则C(
,
),CF=
,DF=OF-OD=
-6=
;
故S△ADC=S梯形AOFC-S△AOD-S△CDF
=
×(3+
)×
-
×3×6-
×
×
=
;
由A(0,3)、D(6,0)得,直线AD:y=-
x+3;
过点P作PQ∥y轴,交直线AD于点Q;设点P(x,
x2-2x+3),则Q(x,-
x+3),PQ=(-
x+3)-(
x2-2x+3)=-
x2+
x;
则S△APD=
×PQ×OD=
×(-
x2+
x)×6=-
x2+
x;
则S四边形APDC=S△ADC+S△APD=-
x2+
x+
=-
(x-3)2+
;
综上,当x=3,即 P(3,-
)时,四边形APDC的面积最大,且最大值为
.
| 1 |
| 4 |
∴
| 1 |
| 4 |
故抛物线的解析式:y=
| 1 |
| 4 |
 (2)由(1)的抛物线解析式知:A(0,3)、D(6,0);
(2)由(1)的抛物线解析式知:A(0,3)、D(6,0);设⊙D与直线BC的切点为E,连接DE,则 DE⊥BE;
∵∠ABC=90°,
∴∠ABO=∠BDE=90°-∠DBE,又∠AOB=∠BED=90°,
∴△AOB∽△BED,有:
| AB |
| BD |
| OB |
| DE |
| ||
| 4 |
| 2 |
| r |
| 8 | ||
|
∴2.2-2<BD<2.2+2,即rD-rB<BD<rD+rB
∴⊙B与⊙D的位置关系为相交.
 (3)过点C作CF⊥x轴于点F,设点C(x,
(3)过点C作CF⊥x轴于点F,设点C(x,| 1 |
| 4 |
| 1 |
| 4 |
同(2)可证得:Rt△AOB∽Rt△BFC,有:
| AO |
| BF |
| OB |
| CF |
| 3 |
| x-2 |
| 2 | ||
|
解得:x1=2(舍)、x2=
| 26 |
| 3 |
则C(
| 26 |
| 3 |
| 40 |
| 9 |
| 40 |
| 9 |
| 26 |
| 3 |
| 8 |
| 3 |
故S△ADC=S梯形AOFC-S△AOD-S△CDF
=
| 1 |
| 2 |
| 40 |
| 9 |
| 26 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 8 |
| 3 |
| 40 |
| 9 |
=
| 52 |
| 3 |
由A(0,3)、D(6,0)得,直线AD:y=-
| 1 |
| 2 |
过点P作PQ∥y轴,交直线AD于点Q;设点P(x,
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 2 |
则S△APD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
| 2 |
则S四边形APDC=S△ADC+S△APD=-
| 3 |
| 4 |
| 9 |
| 2 |
| 52 |
| 3 |
| 3 |
| 4 |
| 289 |
| 12 |
综上,当x=3,即 P(3,-
| 3 |
| 4 |
| 289 |
| 12 |
点评:此题主要考查了函数解析式的确定、相似三角形的应用、圆与圆的位置关系、图形面积的解法以及二次函数的应用等重点知识;在解题过程中要注意数形结合思想的合理应用.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
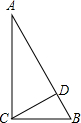 如图,直角三角形ABC中∠ACB=90°,CD是高,∠A=30°,AB=4.则BD=
如图,直角三角形ABC中∠ACB=90°,CD是高,∠A=30°,AB=4.则BD= 如图,直角三角形ABC的直角边AB=6,以AB为直径画半圆,若阴影部分的面积S1-S2=
如图,直角三角形ABC的直角边AB=6,以AB为直径画半圆,若阴影部分的面积S1-S2= 如图在直角三角形ABC的斜边AB上另作直角三角形ABD,并以AB为斜边,若BC=1,AC=m,AD=2,则BD等于( )
如图在直角三角形ABC的斜边AB上另作直角三角形ABD,并以AB为斜边,若BC=1,AC=m,AD=2,则BD等于( ) 如图,直角三角形ACB中,CD是斜边AB上的中线,若AC=8cm,BC=6cm,那么△ACD与△BCD的周长差为
如图,直角三角形ACB中,CD是斜边AB上的中线,若AC=8cm,BC=6cm,那么△ACD与△BCD的周长差为 如图,直角三角形ABC中,∠C=90°,P,E分别是边AB,BC上的点,D为△ABC外一点,DE⊥BC,DE=EC,BE=2EC,∠BDE=∠PEC,AD∥PE,AC=4,则线段BC的长为
如图,直角三角形ABC中,∠C=90°,P,E分别是边AB,BC上的点,D为△ABC外一点,DE⊥BC,DE=EC,BE=2EC,∠BDE=∠PEC,AD∥PE,AC=4,则线段BC的长为