题目内容

已知△ABC中，AB=AC=4 $数学公式$ ，高AD=4，则△ABC的外接圆半径是

A.
3
B.
4
C.
5
D.
6

D
分析：可依据题意作出简单的图形，进而先求出BD的长，进而再由勾股定理求解半径即可．
解答：

解：由于AB=AC，所以其外接圆的圆心在三角形的高上，如图所示，
∵AB=4 $\text{[math]}$ ，AD=4，AD⊥BC，
∴BD= $\text{[math]}$ =4 $\text{[math]}$ ，
可设圆的半径为x，
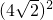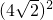则在Rt△BOD中，（4-x）²+ $\text{[math]}$ =x²，解得x=6，
故选D．
点评：本题主要考查了三角形与外接圆的知识以及勾股定理的运用，能够熟练运用勾股定理求解一些简单的直角三角形的计算问题．

练习册系列答案

巧学巧练系列答案

国华作业本名校学案系列答案

全通学案系列答案

轻松作业本系列答案

全解全习系列答案

阳光课堂金牌练习册系列答案

5年高考3年模拟系列答案

经纶学典单元期末冲刺卷系列答案

课课练江苏系列答案

课课通导学练精编系列答案

相关题目

如图，已知△ABC中，AB=AC，AD平分∠BAC，请补充完整过程证明△ABD≌△ACD的理由．
∵AD平分∠BAC，
∴∠BAD=∠

（角平分线的定义）．
在△ABD和△ACD中，

∴△ABD≌△ACD

已知△ABC中，AB=AC，AD为BC边上的中线，BE为AC边上的高，
（1）在图中作出中线AD（要求用尺规作图，保留作图痕迹，不写作法与证明）；
（2）设AD，BE交于点F，若∠ABC=70°，求∠DFB的度数．

已知△ABC中，AB=20，AC=15，BC边上的高为12，则△ABC的周长为

如图，已知△ABC中，AB=AC，AD平分∠BAC，请补充完整过程，说明△ABD≌△ACD的理由．
∵AD平分∠BAC
∴∠

（角平分线的定义）
在△ABD和△ACD中

∴△ABD≌△ACD

如图：已知△ABC中，AB=17cm，BC=30cm，BC边上的中线AD=8cm．求证：△ABC是等腰三角形．