题目内容
一个正方形的内切圆半径、外接圆半径与这个正方形边长的比为( )
A、1:2:
| ||
B、1:
| ||
C、1:
| ||
D、
|
分析:根据题意画出图形,设正方形边长a,连接OA、OB,过O作OE⊥AB,先求出∠AOB的度数,再根据等腰三角形的性质求出∠AOE的度数,由特殊角的三角函数值求出OA、OE的长,再求出两圆及正方形的面积即可.
解答: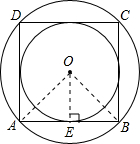 解:如图所示,设正方形边长a,连接OA、OB,过O作OE⊥AB;
解:如图所示,设正方形边长a,连接OA、OB,过O作OE⊥AB;
∵∠AOB=
=90°,OA=OB,
∴∠AOE=
∠AOB=
×90°=45°,
∴AE=OE=
,
OA=
=
=
a,
∴内切圆半径、外接圆半径与这个正方形边长的比为:OE:OA:AB=
:
a:a=1:
:2.
故选B.
 解:如图所示,设正方形边长a,连接OA、OB,过O作OE⊥AB;
解:如图所示,设正方形边长a,连接OA、OB,过O作OE⊥AB;∵∠AOB=
| 360° |
| 4 |
∴∠AOE=
| 1 |
| 2 |
| 1 |
| 2 |
∴AE=OE=
| a |
| 2 |
OA=
| AE |
| sin45° |
| ||||
|
| ||
| 2 |
∴内切圆半径、外接圆半径与这个正方形边长的比为:OE:OA:AB=
| a |
| 2 |
| ||
| 2 |
| 2 |
故选B.
点评:本题考查了正方形的内切圆、外接圆的性质,解答此题的关键是根据题意画出图形,再根据正方形及直角三角形的性质解答.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 B 1∶
B 1∶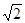 ;
B、1∶
;
B、1∶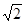 B 1∶
B 1∶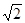 B 1∶
B 1∶