Question

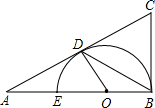如图，已知在△ABC中，∠B=90°．O是AB上一点，以O为圆心，OB为半径的半圆与AB交于点E，与AC切于点D，AD=2，AE=1．求证：S_△AOD、S_△BCD是方程10x²-51x+54=0的两个根．

Answer 1

分析：此题要证明S_△AOD、S_△BCD是方程10x²-51x+54=0的两个根，首先需求得两个三角形的面积，再进一步根据根与系数的关系进行证明．根据切割线定理，即可求得AB的长，从而求得圆的半径，则可以求得三角形AOD的面积；根据勾股定理求得CD的长，再根据相似三角形的性质即可求得BH的长，从而求得三角形BCD的面积．

解答：证明：∵AD是切线，
∴AD²=AE•AB．
由AD=2，AE=1，得AB=4．
从而OD=

3

2

．
∵∠ABC=90°，
∴AC²=BC²+AB²，且BC是⊙O的切线．
∵CD是⊙O的切线，
∴BC=CD．
∴（2+BC）²=BC²+4²，
解得BC=3．
∵OD⊥AD，
∴S_△AOD=

1

2

AD•OD=

1

2

×2×

3

2

=

3

2

．
作BH⊥AC于H，则Rt△AOD∽Rt△ABH．
∴

OD

BH

=

AO

AB

，
即

3 2

BH

=

1+ 3 2

4

，
∴BH=

12

5

．
∴S_△BCD=CD•BH=

1

2

×3×

12

5

=

18

5

．
而S_△AOD+S_△BCD=

3

2

+

18

5

=

51

10

，
S_△AOD•S_△BCD=

3

2

×

18

5

=

54

10

，
∴S_△AOD、S_△BCD是方程10x²-51x+54=0的两个根．

点评：此题综合运用了切割线定理、切线长定理、勾股定理、相似三角形的判定和性质、一元二次方程根与系数的关系．