题目内容
如果在Rt△ABC中,∠C=90°,a=8,b=15,则sinA+sinB+sinC=________.

分析:根据勾股定理求出斜边的长,再由正弦的定义,分别求出∠A,∠B,∠C的正弦值,然后求出它们的和.
解答:由勾股定理有:c=
 =
= =17,于是
=17,于是 ,所以sinA+sinB+sinC=
,所以sinA+sinB+sinC=
故答案是:

点评:本题考查的是锐角三角函数的定义,先用勾股定理求出斜边的长,再用正弦的定义求出∠A,∠B的正弦值,∠C=90°,它的正弦值是1,然后求出它们的和.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
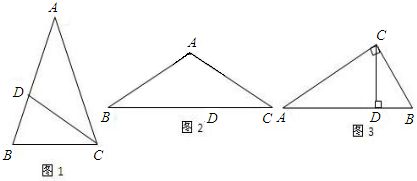
 ,底角平分线与腰的交点为黄金分割点.
,底角平分线与腰的交点为黄金分割点. ,则请你求出∠A的度数;
,则请你求出∠A的度数;