题目内容
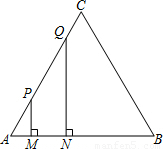
如图①，在长为6厘米，宽为3厘米的矩形PQMN中，有两张边长分别为二厘米和一厘米的正方形纸片ABCD和EFGH，且BC且在PQ上，PB=1厘米，PF=
厘米，从初始时刻开始，纸片ABCD沿PQ以2厘米每秒的速度向右平移，同时纸片EFGH沿PN以1厘米每秒的速度向上平移，当C点与Q点重合时，两张图片同时停止移动，设平移时间为t秒时，（如图②），纸片ABCD扫过的面积为S1，纸片EFGH扫过的面积为S2，AP，PG，GA所围成的图形面积为S（这里规定线段面积为零，扫过的面积含纸片面积）．解答下列问题：（1）当t=
时，PG=______
【答案】分析：（1）PG=
=
，PA=
=2
，AG=
=
，∴PA=PG+GA．
（2）由（1）得当t=0.5时，G在AP上，那么可分G在△APB内和△APB外两种情况进行解答．
（3）按等量关系列出等式，根据t的取值范围得到所求．
解答：解：（1）当t=
时，PG=
，PA=2
，此时PA=PG+GA；（各1分）
（2）①当0≤t≤0.5时，连接GB
S△APG=S△APB-S△PGB-S△AGB
=
×2（2t+1）-
（2t+1）（t+0.5）-
×2×2t
=-t2-t+
（2分）
②当0.5＜t≤1.5时，过A作AK⊥PN于K，连接KG
S△APG=S△APK-S△PGK-S△AGK
=
×2（2t+1）-
（2t+1）（1.5-t）-
×1×2
=t2+t-
（2分）
（3）存在
S1=2（2t+2）=4t+4，S2=t+1（1分）
若S1+S2=4S+5，则
4t+4+t+1=4（t2+t-
）+5，即4t2-t-3=0（1分）
∴t1=
（舍去），t2=1（1分）
即当t=1时，S1+S2=4S+5．
点评：本题考查运动过程中面积的变化形式．注意扫过的面积应是原来正方形的面积+扫过矩形的面积．
=，PA==2，AG==，∴PA=PG+GA．（2）由（1）得当t=0.5时，G在AP上，那么可分G在△APB内和△APB外两种情况进行解答．
（3）按等量关系列出等式，根据t的取值范围得到所求．
解答：解：（1）当t=
时，PG=，PA=2，此时PA=PG+GA；（各1分）（2）①当0≤t≤0.5时，连接GB
S△APG=S△APB-S△PGB-S△AGB
=
×2（2t+1）-（2t+1）（t+0.5）-×2×2t=-t2-t+
（2分）②当0.5＜t≤1.5时，过A作AK⊥PN于K，连接KG
S△APG=S△APK-S△PGK-S△AGK
=
×2（2t+1）-（2t+1）（1.5-t）-×1×2=t2+t-
（2分）（3）存在
S1=2（2t+2）=4t+4，S2=t+1（1分）
若S1+S2=4S+5，则
4t+4+t+1=4（t2+t-
）+5，即4t2-t-3=0（1分）∴t1=
（舍去），t2=1（1分）即当t=1时，S1+S2=4S+5．
点评：本题考查运动过程中面积的变化形式．注意扫过的面积应是原来正方形的面积+扫过矩形的面积．
练习册系列答案
相关题目
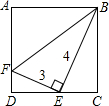如图，一个边长为3、4、5厘米的直角三角形的一个顶点与正方形的顶点B重合，另两个顶点分别在正方形的两条边AD、DC上，那么这个正方形的面积是
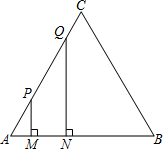已知：等腰三角形ABC的两腰AC和BC长为5厘米，底边AB长为6厘米，如图，现有一长为1厘米的线段MN在△ABC的底边AB上沿AB方向以1厘米/秒的速度向B点运动（运动开始时，点M与点A重合，点N到达点B时运动终止），过点M、N分别作AB边的垂线，与△ABC的其它边交于P、Q两点，线段MN运动的时间为t秒．
