题目内容
 如图,等腰△ABC中,底边BC=a,∠A=36°,∠ABC的平分线交AC于D,∠BCD的平分线交BD于E,设k=
如图,等腰△ABC中,底边BC=a,∠A=36°,∠ABC的平分线交AC于D,∠BCD的平分线交BD于E,设k=
| ||
| 2 |
| A、k2a | ||
| B、k3a | ||
C、
| ||
D、
|
分析:根据三角形特点,先求出角的度数,从而得到三角形相似,再根据相似三角形对应边成比例即可求得.
解答:解:在等腰△ABC中,底边BC=a,∠A=36°
∴∠ABC=∠ACB=72°
∵BD平分∠ABC
∴∠ABD=∠CBD=36°
同理∠DCE=∠BCE=36°
∴∠DEC=36°+36°=72°,∠BDC=72°
∴△CED∽△BCD
故:CD:DE=BD:CE,
设ED=x,BD=BC=a,
∵BC=BD,则BE=CE=CD=a-x,
故BE2=BD•ED,即(a-x)2=ax,
移项合并同类项得x2-3ax+a2=0,
解得x=
a,或x=
a>BD(舍去)
∵k2=(
)2=
∴ED=k2a
故选A.
∴∠ABC=∠ACB=72°
∵BD平分∠ABC
∴∠ABD=∠CBD=36°
同理∠DCE=∠BCE=36°
∴∠DEC=36°+36°=72°,∠BDC=72°
∴△CED∽△BCD
故:CD:DE=BD:CE,
设ED=x,BD=BC=a,
∵BC=BD,则BE=CE=CD=a-x,
故BE2=BD•ED,即(a-x)2=ax,
移项合并同类项得x2-3ax+a2=0,
解得x=
3-
| ||
| 2 |
3+
| ||
| 2 |
∵k2=(
| ||
| 2 |
3-
| ||
| 2 |
∴ED=k2a
故选A.
点评:本题主要考查相似三角形的判定和相似三角形对应边成比例.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
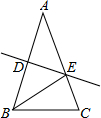 如图,等腰△ABC中,AB=AC,∠A=20°.线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于( )
如图,等腰△ABC中,AB=AC,∠A=20°.线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于( )| A、80° | B、70° | C、60° | D、50° |
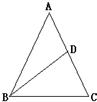 13、如图,等腰△ABC中,AB=AC,BD为腰AC的中线,将△ABC分成长12cm和9cm的两段,则等腰△ABC的腰长为
13、如图,等腰△ABC中,AB=AC,BD为腰AC的中线,将△ABC分成长12cm和9cm的两段,则等腰△ABC的腰长为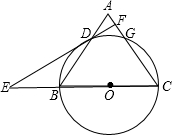 如图,等腰△ABC中,AC=BC=10,AB=12,以BC为直径作⊙0交AB于D,交AC于G,DF⊥AC,垂足为F,交CB的延长线于点E,则sinE=
如图,等腰△ABC中,AC=BC=10,AB=12,以BC为直径作⊙0交AB于D,交AC于G,DF⊥AC,垂足为F,交CB的延长线于点E,则sinE= 如图,等腰△ABC中,AB=AC,D为BC中点,E为射线AD上一点.
如图,等腰△ABC中,AB=AC,D为BC中点,E为射线AD上一点. 如图,等腰△ABC中,AB=AC,D、E分别为AC、AB的中点.
如图,等腰△ABC中,AB=AC,D、E分别为AC、AB的中点.