题目内容
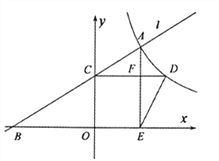
【题目】如图,已知点![]() 是反比例函数
是反比例函数![]() 的图像上的一个动点,经过点
的图像上的一个动点,经过点![]() 的直线
的直线![]() 交
交![]() 轴负半轴于点
轴负半轴于点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() .过点
.过点![]() 作
作![]() 轴的垂线,交反比例函数的图像于点
轴的垂线,交反比例函数的图像于点![]() .过点
.过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .设点
.设点![]() 的横坐标是
的横坐标是![]() .
.
(1)若![]() ,求点
,求点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示);
的代数式表示);
(2)若![]() ,当四边形
,当四边形![]() 是平行四边形时,求
是平行四边形时,求![]() 的值,并求出此时直线
的值,并求出此时直线![]() 对应的函数表达式.
对应的函数表达式.
【答案】(1)(![]() a,
a,![]() );(2)y=
);(2)y=![]() x+3.
x+3.
【解析】
(1)由A点坐标可表示出AE的长,利用相似三角形的性质可求得CO的长,代入反比例函数解析式可表示出D点坐标;
(2)由条件可求得D点坐标,由平行四边形的性质可得△ACF∽△ABE,利用相似三角形的性质可求得a的值,则可求得A点坐标,由A、C的坐标,利用待定系数法可求得直线l的函数表达式.
(1)∵点A的横坐标是a,∴点A的纵坐标为![]() ,∴AE=
,∴AE=![]() ,
,
∵AE⊥x轴,∴CO∥AE,∴△BOC∽△BEA,∴![]() =
=![]() =
=![]() ,∴CO=
,∴CO=![]() ,
,
把y=![]() 代入y=
代入y=![]() ,解得x=
,解得x=![]() a,∴D点坐标为(
a,∴D点坐标为(![]() a,
a,![]() );
);
(2)∵OC=3,∴D点纵坐标为3,把y=3代入y=![]() 可得x=4,∴D(4,3),∴CD=4,
可得x=4,∴D(4,3),∴CD=4,
∵四边形BCDE是平行四边形,∴BE=CD=4,且CD∥BE,∴△ACF∽△ABE,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得a=2,∴A(2,6),且C(0,3),
,解得a=2,∴A(2,6),且C(0,3),
∴可设直线l的函数表达式为y=kx+3,把x=2,y=6代入,可得6=2k+3,解得k=![]() ,
,
∴直线l的函数表达式为y=![]() x+3.
x+3.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目