Question

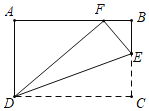
【题目】如图，在矩形中．点从点出发以的速度向点运动，以为一边在的右下方作正方形．同时垂直于的直线从点出发以的速度向点运动，当直线和正方形开始有公共点时，点运动的时间为__________

Answer 1

【答案】

【解析】

首先过点F作FL⊥C于点L,证明△ADE≌△ELF，进而得出AD=EL，得出当直线MN与正方形AEFG开始有公共点时：DL+CM≥16，进而求出即可．

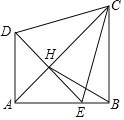
解：如图，过点F作FL⊥CD于点L，

∵在四边形AEFG中，，∠AEF=90°，AE=EF

∴∠AED+∠FEL=90°，

∵∠DAE+∠AED=90°

∴∠DAE=∠FEL

在△ADE和△ELF中

∴△ADE≌△ELF(AAS)

∴AD=EL=6

当直线和正方形开始有公共点时,DL+CM≥16

∴DE+EL+MC≥16,

即t+6+2t≥16

解得：t≥

所以当经过秒时，直线MN和正方形AEFG开始有公共点

故答案为：